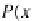Graphics Reference
In-Depth Information
Fig. 9.1
Rotating the point
P
about the
z
-axis
or in matrix form as
R
β,x
⎡
⎤
1
0
0
0
⎣
⎦
0
cos
β
−
sin
β
0
R
β,x
=
.
0 in
β
cos
β
0
0
0
0
1
To rotate about the
y
-axis, the
y
-coordinate remains constant whilst the
x
- and
z
-
coordinates are changed. This is expressed algebraically as
x
=
z
sin
β
+
x
cos
β
y
=
y
z
=
z
cos
β
−
x
sin
β
or in matrix form as
R
β,y
⎡
⎤
cos
β
0 in
β
0
⎣
⎦
01
00
R
β,y
=
.
−
sin
β
0
cos
β
0
00
01
Note that the matrix terms don't appear to share the symmetry enjoyed by the pre-
vious two matrices. Nothing really has gone wrong, it's just the way the axes are
paired together to rotate the coordinates. Now let's consider similar rotations about
off-set axes parallel to the Cartesian axes.
9.2.3 Rotating About an Off-Set Axis
To begin, let's develop a transform to rotate a point about a fixed axis parallel with
the
z
-axis, as shown in Fig.
9.2
. The scenario is very reminiscent of the 2D case for
rotating a point about an arbitrary point, and the general transform is given by
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
x
y
z
1
x
y
z
1
T
t
x
,t
y
,
0
R
β,z
T
−
t
x
,
−
t
y
,
0