Graphics Reference
In-Depth Information
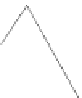
Fig. 7.1
2D homogeneous
coordinates can be visualised
as a plane in 3D space where
t
=
1, for convenience
For our purposes we can imagine that a collection of homogeneous points of
the form
(xt, yt, t)
exist on an
xy
-plane where
t
is the
z
-coordinate as illustrated
in Fig.
7.1
. The figure shows a triangle on the
t
=
1 plane, and a similar, larger
triangle on a more distant plane. Thus, instead of working in two dimensions, we
can work on an arbitrary
xy
-plane in three dimensions. The
t
-coordinate of the plane
is immaterial because the
x
- and
y
-coordinates are eventually scaled by
t
. To keep
things simple it is convenient to choose
t
1, which means that the point
(x, y)
has
homogeneous coordinates
(x, y,
1
)
making scaling unnecessary.
If we substitute 3D homogeneous coordinates for traditional 2D Cartesian coor-
dinates we must attach 1 to every
(x, y)
pair. When a point
(x, y,
1
)
is transformed,
it emerges as
(x
,y
,
1
)
, and we discard the 1. This may seem a futile exercise, but
it resolves the problem of creating a translation transform.
Consider the following transform on the homogeneous point
(x, y,
1
)
:
=
x
=
ax
+
by
+
e
y
=
cx
+
dy
+
f
this is represented in matrix form as
⎡
⎣
⎤
⎦
=
⎡
⎣
⎤
⎦
⎡
⎣
⎤
⎦
x
y
1
abe
cdf
001
x
y
1
and resolves the problem of translation by adding
e
and
f
to
x
and
y
respectively.
However, this has to be paid for in terms of extra memory required to store the larger
matrix.
7.3 Matrix Transforms
In this section we investigate strategies for designing matrix transforms to translate
and rotate points about the origin and an arbitrary point. We will also see how the
inverse transform is used to establish new frames of reference.