Stochastic process fundamentals - Modelling with Generalised Stochastic Petri Nets - page 280

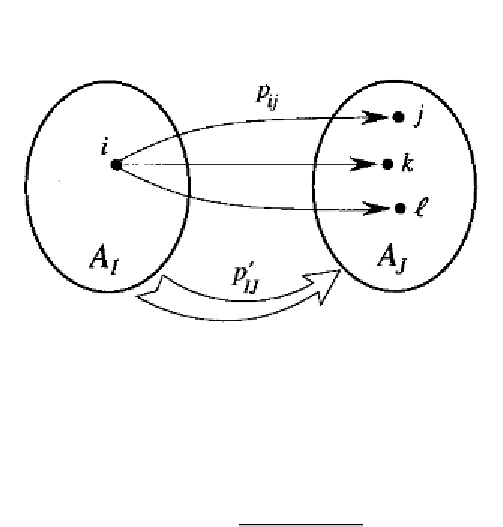
Figure A.7: Transition probabilities between states and macrostates.

where

η i (n)

ν i|I (n) =

P

(A.58)

k∈A I η k (n)

represents the conditional probability of being in state i ∈ A I given that the
process is in macrostate A I . Note that a necessary and su cient condition
for the process { Y n ,n ≥ 0 } to be an ergodic DTMC is that
X

= p 0 IJ (n) p ij (A.59)

j∈A J

for all i ∈ A I , and for all n. Indeed, in this case the conditional probabilities
( A.56) depend only on the present (macro)state, and the dependence on n
in ( A.57) and ( A.58) disappears.
Condition ( A.59) is the lumpability condition of the DTMC { X n ,n ≥ 0 }
with respect to the partition S 0 . The DTMC { Y n ,n ≥ 0 } is then called the
lumped Markov chain.
If only the steady-state behavior is of interest, it is possible to write for the
DTMC { X n ,n ≥ 0 }

X

η j = η i p ij (a)

i∈S

(A.60)

X

η j = 1 (b)

j∈S

Summing (A.60a ) over all states j in macrostate A J , we obtain

X

η 0 J = η 0 I p 0 IJ (A.61)

A I ∈S 0