Biology Reference
In-Depth Information
It is obvious from previous discussions that we are playing down the
importance of hypothesis testing. While providing these testing proce-
dures in order to offer a more complete set of tools, our ultimate goal is to
present methods for examining
how
two growth patterns differ or coin-
cide with one another. Specifically, we want to
localize
these similarities
and differences to anatomical complexes. The identification of specific
structures enables interpretation of the biological mechanisms that
might underlie these differences. This information could ultimately be
used to propose explanatory hypotheses.
There are several ways to localize the difference in growth patterns to
anatomical positions. The simplest, but most time-consuming way, is to
simply study the individual
GMs
for the samples of interest and the
GDM
. In addition, non-parametric confidence intervals can be calculated
for growth differences local to each linear distance following methods
similar to those developed for studying form and shape difference
(
Chapter 4
).
Since confidence intervals are not one-way in nature, all four samples
in a growth analysis are used to create the bootstrapped samples.
Continuing with the previous notation using samples
A
1
, A
2
, B
1
, B
2
of size
m
,
n
,
o
, and
p
, respectively, we obtain a sample of size
m
from
A
1
and of size
n
from
A
2
using a random sampling design with replacement. Similarly
we obtain simple random samples with replacement of size
o
from
B
1
and
of size
p
from
B
2
.A
GDM
is calculated from these bootstrapped samples
and then sorted according to the landmarks that define the linear dis-
tance. This is done
B
times. A collection of boot-strapped samples sorted
in this way has rows and
B
columns in matrix format. Each
column is a growth difference matrix for a set of bootstrapped samples
and each row represents B growth difference matrix ratios for a
defined linear distance. To obtain a confidence interval for each linear
distance, the ratios in each row are sorted in increasing order. If a 10%
confidence interval is sought, then the first 5% (those of minimal
value) and the last 5% (those of maximum value) of the total entries in
the row are deleted. The minimum and maximum entries remaining in
that row constitute the minimum and maximum values for a bootstrap
confidence interval for the linear distance under consideration. As in
the confidence intervals for the study of form (
Chapter 4
), the collec-
tion of confidence intervals for all linear distances that constitute a
growth difference matrix does not represent a confidence band for
growth of the form. These represent marginal confidence intervals cal-
culated separately for each linear distance.
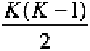
Search WWH ::

Custom Search