Biology Reference
In-Depth Information
5.7 Statistical analysis of form and shape difference due
to growth
As discussed in previous sections, although statistical testing is a stan-
dard part of any quantitative analysis of morphology, it should not be
considered the definitive answer to questions concerning similarity of
growth patterns. If
GDM (A
2
,A
1
: B
2
,B
1
)
does not equal 1, patterns of dif-
ferences from 1 should be sought by close examination of the
GDM
.
This process is labor intensive but graphic aids are available (some of
which are discussed in
Chapter 4
; also see Cole and Richtsmeier, 1998).
To test for the statistical significance of differences in shape change
due to growth we use the statistic
G
obs
:
where max (= maximum) is the ratio with the largest value within the
GDM
, and min (= minimum) is the ratio with the smallest value. This
test statistic is scale invariant thereby eliminating the effects of scal-
ing. Growth patterns are interpreted as being more similar in shape
change as
G
obs
approaches 1. A null hypothesis of similarity in shape
change due to growth is stated as:
H
o
:GM
ij
(
A
2
,A
1
) = c
GM
ij
(
B
2
, B
1
)
where
c
is some scaling factor and
c >
0. This is a one-way hypothesis
that states that the growth of sample
B
is similar to the growth of sam-
ple A. If accepted, it does not imply that the growth of sample
A
is
similar to the growth of sample
B
. This would have to be tested by
restating the null hypothesis as:
H
o
:GM
ij
(
B
2
,B
1
) = c
GM
ij
(
A
2
, A
1
)
and rerunning the analysis using the other sample as the base population.
The one-way nature of this hypothesis demands a specific design
for the statistical testing of
G
obs
. Our design uses an extension of the
bootstrap approach presented in
Chapter 4
. The statistical comparison
of growth patterns from two populations using a one-way hypothesis
requires that one of the samples be chosen to represent the base pop-
ulation. The choice of which sample to use as the base population can
be made for statistical reasons (e.g., the sample with the largest num-
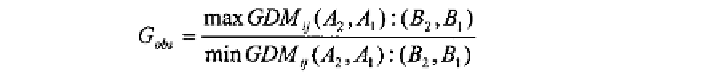
Search WWH ::

Custom Search