Biology Reference
In-Depth Information
1)/2
. The above theorem provides a characterization of this sub-
set of the
K
(
K
K
(
K
1)/2
dimensional Euclidean space that corresponds to
forms of
K
-landmark,
D
-dimensional objects. We call this subset “the
form space of
K
-landmarks,
D
-dimensional objects” or “the form space,”
for short.
Suppose now that we are given a point
d
from the form space. How
do we obtain the landmark coordinates of the corresponding object? It
is clear that the mapping from the form space to the space of landmark
coordinate matrices is not one-to-one. A single point in the form space
maps onto a single orbit, which is, in fact, a collection of several matri-
ces, in the space of landmark coordinate matrices. Thus, corresponding
to a single point in the form space, there is a unique orbit in the land-
mark coordinate matrix space and conversely, corresponding to a given
orbit there is a unique point in the form space. For a discussion of
orbits or equivalence classes, see
Chapter 3
or the first part of this
chapter. In the following, we show how to map a given point in the form
space to a particular member of the corresponding orbit. Once such a
member is obtained, one can rotate, reflect, or translate it to obtain any
other member in the orbit.
Let
d
be a point in the form space. Calculate
B
d
. Consider the spec-
tral decomposition of the matrix
B
d
, namely,
B
d
P
T
. Because the
rank of matrix
B
d
is
D
and is positive semi-definite, there are D non-
zero eigenvalues. Let
1
,
P
D
be the eigenvalues and let
P
(1)
,
P
(2)
,…,
P
(
D
)
be the corresponding eigenvectors. Construct a
K
2
,…,
D
matrix as follows: This matrix is
a landmark coordinate representation of the object corresponding to
d
.
If we calculate the form matrix corresponding to
A
d
, namely the matrix
of all possible pairwise distances between these landmark coordinates,
it exactly equals
d
.
The results above provide a way to transform a landmark coordi-
nate representation to the form matrix representation and vice versa.
4.19 Statistical properties of the estimators of
mean form, mean form difference, and mean shape
difference matrices
Under the Gaussian perturbation model described in
Chapter 3
, we
show that the mean form difference and mean shape difference matri-
ces can be estimated consistently.
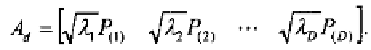

Search WWH ::

Custom Search