Biology Reference
In-Depth Information
Relative form difference
The relative difference between forms is another useful way of describ-
ing form difference in biological objects. When written as a matrix, the
collection of relative differences is called the form difference matrix.
Our emphasis on this particular expression of form difference has
resulted in the following notation,
, where
FDM (B,A)
elements of the form difference matrix correspond to the ratios of like-
linear distances, and the division is done element-wise (where
0
0
by definition). Continuing with the data sets described above, the form
difference matrix for forms A and B is written:
0
02 1
20
FDM B A
(, )
.
9
1
1 59
.
0
Because form difference matrices are square, symmetric matrices
with zero along the diagonal, only the above diagonal elements are
needed to describe the form difference. As a matter of convention, we
write the form difference matrix in vector form, where only the above-
diagonal elements are reported:
2
1
159
FDM B A
(, )
.
Scaling factors and differences in scaled forms
In many biological studies, it is helpful to adjust for size differences
according to some scaling factor before comparison. Within the context
of landmark coordinate data, one can use various measures as scaling
factors. For example, a specific biological distance might be used, or the
geometric mean of all distances could be used as a scaling factor.
Mosimann (1979) provided a general mathematical definition of scal-
ing factor and referred to scaling factors as a measure of 'size.'
Following these ideas, the scaled form is referred to as 'size-corrected.'
Comparison of size-corrected forms is often considered a comparison of
'shapes.'
Following Mosimann (1979), we consider any function of the dis-
tances that always takes a positive value as a scaling factor. However,
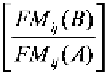
Search WWH ::

Custom Search