Biology Reference
In-Depth Information
STEP 5:The estimate of the coordinates of the mean form is given by:
This can be used to calculate the form matrix by calculating the dis-
tances between the three landmarks.
The estimate of the covariance matrix
K
*
K
L
T
is given by
L
and the estimate of the eigenvalues of
D
is given by
Generalization of this algorithm to three-dimensional objects and
objects with more than 3 landmarks is notationally complicated but
straightforward. We do not provide the details here.
3.14.2 Generating observations using the estimated mean form and
the covariance matrix
I
D
in
detail. This is the model that is extensively used throughout this mono-
graph. The following algorithm is described for a two-dimensional
object. Generalization to three-dimensional object is straightforward.
Let
M
K
-1
be a submatrix consisting of the first (
K
-1) rows of
M
, the
mean form coordinate matrix obtained in Step of Algorithm 1. Let
K
-1
*
denote the (
K
-1)
(
K
-1) submatrix of
K
*
. This matrix consists of the
first (
K
-1) rows and (
K
-1) columns of
K
*
. In general,
K
-1
*
should be a
positive definite matrix. The non-positive definiteness of
K
-1
*
implies
that the sample size is much too small to fruitfully conduct any statis-
tical analysis, see the discussion in
Part 1
of this chapter.
We will describe the algorithm for the covariance model
K
Algorithm for generating matrix normal random variates
STEP 1: Obtain the Cholesky decomposition of
K
-1
*
. That is,
obtain an upper triangular matrix
C
such that
K
-1
*
CC
T
.
STEP 2: Generate
2
(
K
-
1
) random numbers from
N
(0,1)
distri-
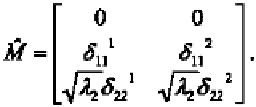




Search WWH ::

Custom Search