Biology Reference
In-Depth Information
STEP 2:Calculate whereD is
the dimension of the observations.
The estimator obtained above, although square and symmetric, is
not guaranteed to be positive semi-definite. One can obtain a positive
semi-definite version using the following steps.
STEP 3: Calculate the spectral decomposition of the matrix
ˆ
K
*
. That is, find its eigenvectors and eigenvalues and write it
as
ˆ
PDP
T
where matrix
D
is a diagonal matrix with the
diagonal elements corresponding to the eigenvalues of
K
*
.If
there are any negative elements in
D
, replace them by zero
and call this modified matrix
~
D
. Obtain a new matrix
K
*
K
*
P
~
DP
T
. This matrix is guaranteed to be square, symmetric, and
positive semi-definite.
Algorithm 2
In this section, we provide an algorithm for the estimation of the mean
form and the covariance structure when we expect that the perturba-
tions along the x, y, and z axes are correlated with each other. We
provide the algorithm for the two-dimensional three landmarks case in
detail. More general situations can be developed using the description
plex models, larger sample sizes are needed to obtain reasonable
estimates. Thus, although more realistic, in practice, this general
model might be more difficult to fit.
Define a matrix
Let
X
c
LX
denote the centered matrices. This centering is slightly
different than the one used in the previous algorithm.
Let
K
K
L
T
and
D
denote a diagonal matrix consisting of the
eigenvalues of
D
.
It was proven in
Part 2
that these are the only estimable quantities
related to covariance.
L
Define a new matrix
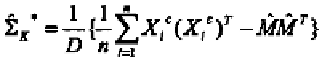
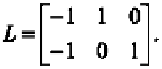
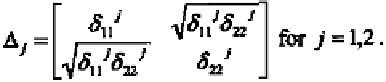


Search WWH ::

Custom Search