Biology Reference
In-Depth Information
In the following, we provide detailed computational algorithms for
estimation of the mean form matrix and variance-covariance matrix.
In order to program these algorithms, the reader will need to under-
stand the following concepts and related computation procedures:
Form matrix, Centered landmark coordinate matrix, Centered inner
product matrix, Eigenvalues, and Eigenvectors. Except for the concepts
of eigenvalues and eigenvectors, all other concepts are described below.
For details on eigenvalues and eigenvectors of a square, symmetric
matrix, refer to any standard matrix algebra textbook such as Barnett
(1990). For computational algorithms, see Press et al., (1986).
Definition of a centered landmark coordinate matrix:
Let
A
be a
landmark coordinate matrix. First, calculate the mean of the
first column and subtract it from all the elements of the first col-
umn; calculate the mean of the second column and subtract it
from all the elements of the second column, and calculate the
mean of the third column and subtract it from all the elements
of the third column. The resultant matrix, denoted by
A
c
,is
called the centered landmark coordinate matrix.
For example, let the landmark coordinate matrix be
Then the centered landmark coordinate matrix is given by subtracting
from each of the entry in a column by the average of the corresponding
column in the landmark coordinate matrix
A.
Thus
is the centered landmark coordinate matrix.
Notice that the column sum of
A
c
is always 0. Notice that this matrix
is obtained when one shifts the original triangle such that its centroid,
instead of matching landmark 1, matches with (0,0).
Centered inner product matrix:
Let
A
c
be a centered landmark
coordinate matrix. Define a new matrix
B
A
c
(
A
c
)
T
. This matrix
is called the centered inner product matrix corresponding to
A
.
The centered inner product matrix corresponding to the above
example is given by
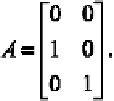
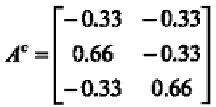


Search WWH ::

Custom Search