Geology Reference
In-Depth Information
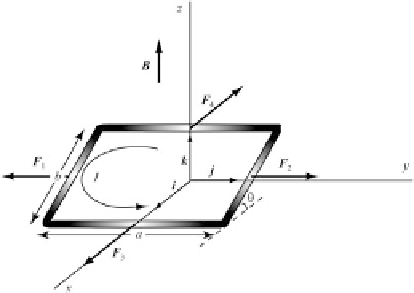
Fig. 3.4
A coil crossed by a current
I
is subject to a net
torque when it is placed in a magnetic field
Fig. 3.3
An electric charge in motion through an homo-
geneous magnetic field follows a helical trajectory
magnitude and are opposite each other (Fig.
3.4
).
Conversely, forces
F
3
and
F
4
, which are applied
to the sides aligned with the
y
direction, also have
the same magnitude, but are not lined up. There-
fore, they generate a force couple that tends to
align the coil with the
xy
plane. Since
F
3
D
IaB
i
,
and
F
4
D
IaB
i
, then the total torque is given by:
Applying the initial conditions we can solve
for the amplitude,
A
, and the phase parameter, ®:
q
v
x0
C
v
y0
I
®
D
arctan
v
x0
v
y0
(3.12)
A
D
Therefore, the particle will follow a helical
trajectory with radius
A
/ (Fig.
3.3
). This impor-
tant example explains why charged particles that
move in the Earth's magnetic field travel in spiral
paths about the geomagnetic field lines.
b
2
F
3
sin ™i
C
b
2
F
4
sin ™i
D
SIB
sin ™i
(3.14)
N
D
where
S
D
ab
. Assuming that
S
is a vector
orthogonal to the coil and having magnitude
S
,
we can introduce a vector
m
such that:
m
D
I
S
.In
this instance, (
3.14
) can be rewritten as follows:
3.2
Magnetic Moments
Let us consider now a rectangular coil having
sides
a
and
b
, placed in a homogeneous magnetic
field
B
D
B
k
(Fig.
3.4
). Let us also assume
that the sides having length
a
are aligned with
direction
y
, and that the coil is inclined by an
angle ™ with respect to the horizontal plane. If
I
is
the current flowing in clockwise sense along the
coil, then the magnetic force (Eq.
3.5
)exertedon
a coil element with orientation
n
and length
dl
is
given by:
N
D
m
B
(3.15)
The vector
m
is called
magnetic moment
of
the coil. Equation
3.15
has general validity and
does not depend from the specific geometry of
the coil. It implies that the field exerts a torque
that tends to align the magnetic moment to the
external field. Let us consider now the example
of an electron that is moving along a circular
orbit with radius
r
with velocity
v
(Fig.
3.5
). If
T
is the orbital period, then the quantity of charge
that crosses an arbitrary surface orthogonal to the
orbit in a unit time is:
dF
D
dq.
v
B/
D
Idl
.n
B/
(3.13)
We can integrate this formula to calculate
the forces exerted on the coil. The forces on
the inclined sides,
F
1
and
F
2
,havethesame
dq
dt
D
e
T
D
e
2 r=
v
D
e
v
2 r
I
D
(3.16)