Geology Reference
In-Depth Information
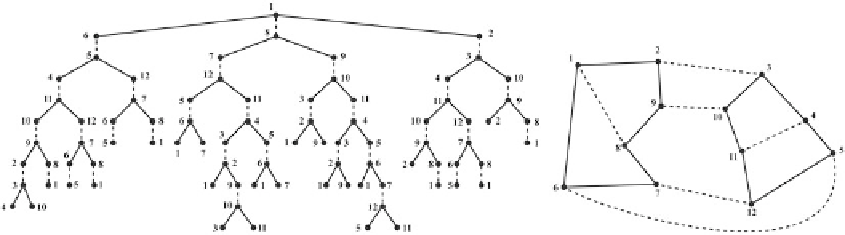
Fig. 2.33
An example of global plate configuration, and the corresponding tree of alternate paths starting from node
J
1
.
Dashed
and
solid lines
are respectively free and conjugate plate boundaries
paths starting from a node. The tree is built setting
the root node as the start node,
s
, and generating
all the possible alternate paths originating in
s
by a modified depth-first search or breadth-first
for the graph of Fig.
2.33
we could start from
node
J
1
, then reach nodes
J
2
,
J
6
,and
J
8
.From
node
J
2
, we must proceed to node
J
3
, while from
J
8
we can proceed either to node
J
7
, or node
J
9
, etc. When one of the edges that are split
in the process of nucleation of a new tectonic
plate is a free boundary, the new intermediate
boundary separating the original plate cannot be
a free boundary. More precisely, it
could
be a
free boundary, but this would not be the minimum
energy solution. In fact, Fig.
2.32
shows that after
insertion of the new triple junctions
J
0
and
J
00
,
only one of the two arms of a free boundary
needs to be converted to a conjugate boundary
after splitting (the boundary between
J
0
and
J
n
in the example of Fig.
2.32
), whereas any other
solution would imply a local reorganization in-
volving more conversions. However, even in this
case the conversion of part of the former free
boundary induces a series of concatenate transi-
tions from free to conjugate boundaries and vice
versa that may propagate outside the perimeter
of the splitting plate, determining a total rear-
rangement of the plate configuration. For each
boundary conversion, another boundary incident
with the same triple junction must be subject to
the inverse of that transformation. At the same
time, a stage boundary is created, which could
either close an existing stage or start a new one
after a time interval of complex relative motion.
The simplest way to terminate the sequence of
boundary conversions and establish a new equi-
librium is to reach the opposite triple junction,
J
00
, along the shortest alternate path. This path
will include an even number of edges when only
one of the splitting boundaries is a free boundary,
whereas an odd number of edges are converted
when two free boundaries are split. The examples
of Fig.
2.34
illustrate these two possibilities.
It should be noted that the new boundary
linking
J
0
and
J
00
, and the alternate path linking
these nodes form a closed loop in
G
, whose
outgoing edges are unaffected by the boundary
conversions. In the case of an even number of
converted edges, for each conjugate boundary
that is transformed into a free boundary there is
a free boundary that is converted into a conju-
gate boundary. Therefore, after the creation of
a new free boundary and two new conjugate
boundaries the total number of edges does not
change. This implies that also in this case
f
and
c
increase respectively by one and by two
units, thereby Eqs. (
2.54
)and(
2.55
) remain valid
and the theorem is proved. When the number of
converted boundaries is odd, after the creation
of two new free boundaries (see Fig.
2.34
)and
one additional conjugate boundary the sequence
of conversions allows an extra conversion of the
last free boundary into a conjugate edge, thereby
during the conversions
f
decreases by one and
c
increases by one. Therefore, also in this case
f
and
c
increase respectively by one and by two
units, so that Eqs. (
2.54
)and(
2.55
) conserve their
validity after the formation of the new plate. This
proves the topological theorem.