Geology Reference
In-Depth Information
has been visited, in which case the algorithm
terminates. The procedure described above can
be easily implemented in recursive form, because
the backward steps imply the use of a
stack
where the address of starting depth search nodes
is stored. Below we present a variant of the classic
algorithm, which can be used to generate a map of
the distances of all the nodes of
G
from a starting
node
x
. This algorithm represents the basis for
building more complex procedures that analyze
properties of graphs.
1:
d
(
x
,
y
)
i
2:
8
z
2
I
(
y
),
dfs
(
z
,
i
C
1)
g
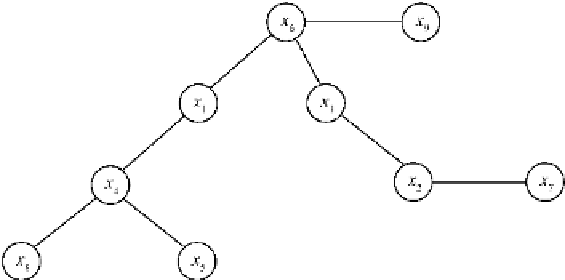
A2.3 Trees
Trees
represent a fundamental class of data struc-
tures, characterized by the absence of cyclic paths
and by connectivity. Therefore, a tree can be de-
fined as an acyclic connected graph (Fig.
A2.5
).
The nodes having unit degree are called
terminal
nodes
or
leaves
, while the remaining vertices
are called
internal nodes
. An interesting property
of the trees is that removal of a single edge is
sufficient to separate the data structure into two
disjoint parts. This feature implies the lowest
degree of connectivity for a graph. The following
theorems determine the fundamental properties
of this important class of graphs.
Algorithm
A2.4
dfss
(
x
):
Depth-first
search
from a node
x
(shell).
Input:
x
2
D
Output:
d
(
x
,
y
)
8
y
2
D
f
0:
8
y
2
D
,
d
(
x
,
y
)
1
1:
dfs
(
x
,0)
g
Algorithm A2.4 represents a shell from which
we call the ricorsive procedure of DFS. It initial-
izes the distance of all the nodes of
G
(including
x
) to infinity, which means “unreachable”. At
the next step, the algorithm calls the recursive
procedure
dfs
() listed below, thereby triggering
the depth search sequence within
G
.
Theorem A2.1
A graph G is a tree iff any pair
of nodes is joined by a unique path
.
Proof
By definition
G
is connected. Conse-
quently, any pair of nodes is joined by at least
one path. However, if two nodes
x
and
y
were
joined by two or more distinct walks,
G
would
have cyclic paths, which would contradict the
hypothesis that
G
is a tree. Let us assume now
that any pair of nodes in
G
is joined by a unique
path. In this instance,
G
is clearly a connected
graph. Furthermore, if we could find a cyclic path
passing through two nodes
x
and
y
, then these
two elements would be joined by distinct paths,
Algorithm
A2.5
dfs
(
y
,
i
):
Depth-first
search
from a node
y
(recursive version).
Input:
y
2
D
,
i
2
N
Output: None
f
0:
d
(
x
,
y
)
i
)
stop
Fig. A2.5
An example of
tree of order 9