Geology Reference
In-Depth Information
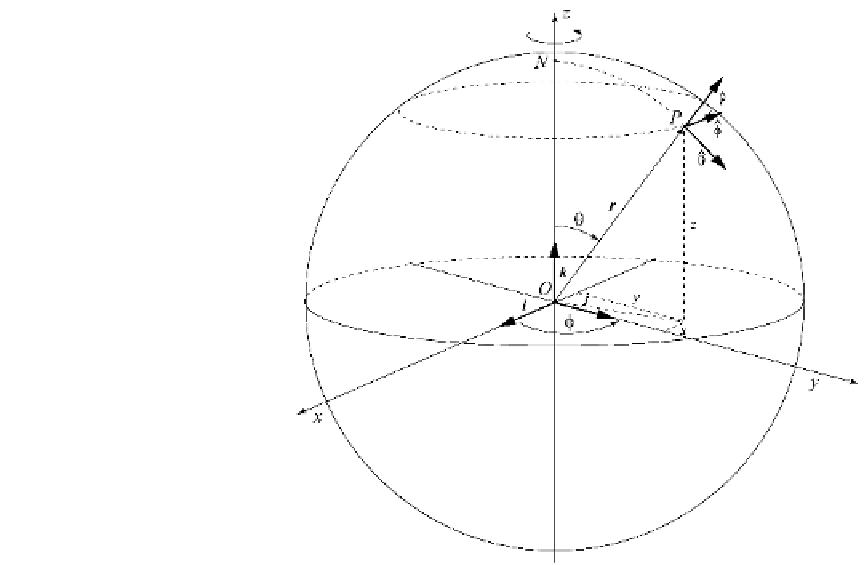
Fig. A1.7
Base versors for
the transformation from
Cartesian to spherical
derivatives
fundamental theorem of vector calculus, which
allows to convert a surface integral into a closed
loop line integral.
A1.4 Spherical Coordinates
Spherical coordinates are a very common
way to represent positions in Earth Sciences.
Figure
A1.7
shows the relation between Carte-
sian, (
x
,
y
,
z
), and spherical, (
r
,™,¥), coordinates
associated with a position vector
r
.
The general transformation rule of vector
fields and differential operators from Cartesian to
spherical coordinates requires the introduction
of the three orthogonal versors
Stokes' Theorem
Let S be a parametric surface with boundary
C
(
S
)
. Then, for every vector field
A
D
A
(
r
),
it
results:
Z
I
r
A
dS
D
A
dr
r, ™,and¥
(Fig.
A1.7
), which are directed respectively
toward increasing distance from the origin,
increasing colatitude (that is, southward),
and increasing longitude (i.e., eastward) at
point
P
(
x
,
y
,
z
). It is easy to prove that the
transformation from the base (
i
,
j
,
k
) to the base
(
(A1.17)
S
C.S/
Another important theorem of vector analy-
sisisthefollowing
Gauss' theorem
, which al-
lows to convert a volume integral into a surface
integral.
r, ™, ¥) is given by:
Gauss (or Divergence) Theorem
2
3
2
3
2
3
r
™
¥
sin ™ cos¥ sin ™ sin ¥ cos™
cos ™ cos ¥ cos™ sin ¥
sin ™
sin ¥
i
j
k
4
5
D
4
5
4
5
Let
R
<
3
, bounded by the
closed surface S
(
R
)
. Then, for every vector field
A
D
A
(
r
),
it results:
Z
3
be a region of
<
cos ¥
0
(A1.19)
I
r
AdV
D
A
dS
(A1.18)
The transformation matrix in (
A1.19
)isan
orthogonal matrix, thereby its inverse is simply
R
S
.
R
/