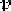Geology Reference
In-Depth Information
8
<
@x
C
ǜ
@
2
u
@
z
2
Z
Z
@
2
u
B
B
@P
@x
2
C
D
0
ˆ.A;B/
D
.
v
n/dr
D
.
u
d
z
- dx/
@
z
C
ǜ
@
2
(13.69)
@
2
@
z
2
@P
:
A
A
@x
2
C
D
0
@§
@
z
d
z
C
@x
dx
Z
B
@§
D
Substituting the stream function gives:
8
<
A
@x
C
ǜ
@
3
§
@
z
3
@
3
§
@P
Z
Z
B
B
@x
2
@
z
C
D
0
D
r
§
dr
D
d§
D
§.B/
§.A/
@
z
ǜ
@
3
§
(13.70)
@
3
§
@
z
2
@x
@P
:
@x
3
C
D
0
A
A
(13.65)
We can eliminate the pressure term from these
equations and obtain a single differential equation
for § taking the partial derivative of the first equa-
tion with respect to
z
and the partial derivative
of the second equation with respect to
x
. Then,
subtracting the resulting equations gives:
Therefore, the change of the stream function
between two points is equal to the areal flow rate
across
any
path linking the two points. In the
case that the path coincides with a streamline,
there is no flux through the curve, because by
definition the velocity is always tangent to a
streamline. Consequently, a fundamental prop-
erty of the stream function is that it is invariant
along streamlines. Another important property is
associated with the
vorticity
of the velocity field.
In general, this is a vector field defined as follows:
@
4
§
@x
4
C
2
@
4
§
@
4
§
@
z
4
Dr
4
§
D
0 (13.71)
@x
2
@
z
2
C
Therefore, the stream function is biharmonic.
It is common practice in geodynamics to display
flow fields through sets of streamlines, which are
usually chosen in such a way that the variation
•§ between neighbouring streamlines is constant.
With this convention, in so far as the distance
d
between two streamlines increases, the velocity
decreases, because
v
•§/
d
. Finally, it is of-
ten useful to express the components of a two-
dimensional velocity field in polar coordinates
(
r
,™). In this instance, the relation between stream
function and velocity components (
u
r
,
u
™
)is:
¨
Dr
v
(13.66)
In the case of case of a two-dimensional field,
this is a vector in the invariant
y
direction:
@
v
@x
@
u
@
z
¨
D
j
j¨
y
(13.67)
Therefore, substituting the definitions (
13.63
)
it results:
@
2
§
@x
2
C
@
2
§
@
z
2
Dr
1
r
@§
@™
I
u
™
D
@§
@r
u
r
D
2
§
(13.72)
¨
y
D
(13.68)
Two-dimensional modelling through stream
functions has been widely used in geodynamics
because of its simplicity and because some com-
plex flows can be represented by superposition
of elementary model flows. The most simple
model is a
uniform flow
in which the streamlines
are parallel each other (Fig.
13.8
).
Source
and
sink flows
are purely radial outward or inward
flows, respectively. The
This expression implies that when the stream
function is a harmonic function, then the flow is
irrotational, thereby
v
is a potential field. Now
let us consider the Navier-Stokes Eq. (
13.13
)and
assume that the inertial term
P
v
can be neglected
because of the very low accelerations. In this in-
stance, introducing the variable
P
(
x
,
z
)
p
(
x
,
z
)-
¡
gz
, we have that in the two-dimensional case the
equations can be rewritten as follows:
velocity is everywhere