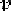Geology Reference
In-Depth Information
•q
dT
•q
dp
13.4
Flow in the Asthenosphere
•q
D
dT
C
dp
p
T
D
c
p
dT
C
T
@s
@p
Now we are going to consider some simple ap-
plications of the equations of fluid dynamics to
the study of the Earth's mantle. In particular, the
objective is to provide physical insights regarding
the behavior of the upper mantle, which has direct
influence on plate motions, despite the extreme
computational difficulty associated with the nu-
merical solution of these equations in more real-
istic applications. In the following, we will focus
our attention on the Earth's asthenosphere, and
we will search analytic solutions of the Navier-
Stokes equations in simple situations, such that
thermodynamic considerations can be neglected.
Let us assume that that a one-dimensional steady
flow of asthenosphere material, considered as a
Newtonian incompressible fluid, exists in a space
of constant thickness
h
between the lithosphere
and the transition zone (Fig.
13.2
).
We also assume that the lithosphere moves at
constant velocity
v
0
relative to the transition zone
(Fig.
13.2
). As discussed in the previous section,
the no-slip boundary condition requires that the
velocity field vectors just below the LAB has
magnitude
v
0
, while the velocity is zero at the
lower boundary with the transition zone. With the
conventions used in Fig.
13.2
, a velocity vector
v
has components
v
(
v
x
(
z
),0,0) for 0
z
h
.
Therefore, the stress tensor has components:
dp
T
'T
¡
dp
D
c
p
dT
(13.36)
where
c
p
is the specific heat per unit mass at
the
specific entropy
(entropy per unit mass). In
this expression, we have assumed again that the
process is reversible, so that •
q
D
Tds
by the
second law of thermodynamics. Substituting into
(
13.35
)gives:
'T
¡
dp
pd
d
u
D
c
p
dT
(13.37)
Now, by the continuity Eq. (
13.7
), the material
derivative of the specific volume
can be calcu-
lated as follows:
1
¡
d
dt
D
d
dt
1
¡
2
d¡
dt
D
1
¡
r
v
D
(13.38)
Therefore, by (
13.37
) the material derivative
of the internal energy per unit mass will be
given by:
2
3
du
dt
D
c
p
dT
'T
¡
dp
dt
1
¡
p
r
v
dt
(13.39)
p0
v
x
=@
z
0
p0
ǜ@
v
x
=@
z
0
4
5
£
D
(13.42)
p
Finally, substituting into (
13.33
)givesthefinal
canonical form of the energy balance equation:
In this expression, the pressure
p
is assumed
to be a function of
x
and
z
only:
p
D
p
(
x
,
z
).
¡c
p
T
'T p
D
ˆ
C
k
r
2
T
C
¡H (13.40)
This equation holds in the hypothesis that the
coefficient of thermal conductivity
k
is constant
throughout the mantle. In the more general case
of variable
k
, the law of conservation of energy
will assume the following form:
k
@T
@x
i
@
@x
i
¡c
p
T
'T p
D
ˆ
C
C
¡H
Fig. 13.2
A Poiseuille-Couette viscous flow in the as-
thenosphere (in the case of
active
drag)
(13.41)