Geology Reference
In-Depth Information
amplitude depends from the inverse square root
of the ray tube cross-section. To determine the
constant
c
, let us consider again the transport
equation in the form (
9.9
). Multiplying this equa-
tion by
A
(
r
), it is possible to rewrite it in the form:
r
A
2
.r/
r
T.r/
D
0
(9.34)
Let us consider two points
r
0
and
r
00
of a
seismic ray and the corresponding wavefronts
T
D
T
0
and
T
D
T
00
. A tube segment between
r
0
and
r
00
is a region
R
bounded by the two wavefronts
and by the tube walls. We know that the gradients
of
T
are always parallel to the lateral surface
of the tube and perpendicular to its end faces.
Therefore, integrating (
9.34
) over the region
R
we have:
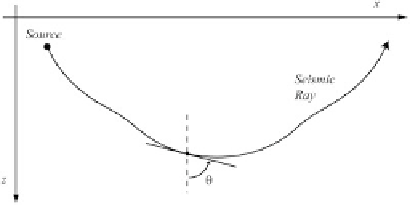
Fig. 9.4
Typical geometry of a seismic ray in a material
where the velocity
c
depends only from depth. ™ is the
incidence angle
p
D
k
s.
z
/
d
d—
(9.38)
is an
invariant
of the seismic ray. In fact, by the
ray Eq. (
9.18
)wehave:
Z
R
r
A
2
.r/
T .r/
dV
s.
z
/
d
d—
0
D
r
d
d—
D
k
d
d—
D
k
r
s.
z
/
D
0
I
I
(9.39)
A
2
.r/
A
2
.r/s.r/dS
D
r
T .r/
dS D
.
R
/
.
R
/
The definition (
9.38
) implies that
p
is normal
to the direction of propagation, thereby any ray
will lie in a vertical plane. Furthermore, the
conservation of
p
requires that also its magnitude
must be constant. Let us define the
incidence
angle
™
D
™(
z
) as the angle that a seismic ray
forms with the vertical at any point (Fig.
9.4
).
The magnitude of
p
is called the
ray parameter
and is a fundamental invariant in seismology,
because it is uniquely associated with a seismic
ray. By (
9.38
) this quantity satisfies the following
simple law:
A
2
.r
00
/s.r
00
/dS.r
00
/
A
2
.r
0
/s.r
0
/dS.r
0
/
(9.35)
D
Hence:
A
2
r
0
s
r
0
dS
r
0
D
A
2
r
00
s
r
00
dS
r
00
(9.36)
By (
9.26
), we also know that the cross-
sections of a tube can be expressed in terms
of geometrical spreading
J
. Therefore, if we have
determined the quantities
A
and
J
at some point
r
D
r
0
, then we can determine the amplitude at
any other point rewriting (
9.33
) as follows:
p
D
s.
z
/ sin ™.
z
/
(9.40)
s
J.
r
0
/s.
r
0
/
J.r/s.r/
The conservation law (
9.40
)for
p
along a
seismic ray is known as
Snell's law
. It allows
to determine the geometry of any sesimic ray
given a velocity function
c
D
c
(
z
)anda
take
-
off
angle ™
0
, which is the incidence angle at the
source point. Clearly, (
9.40
) results from a flat-
Earth approximation that is adequate only in the
case of shallow propagation, say up to 30 km
depth. In a spherical Earth with radial symmetry,
the slowness
s
and the incidence angle ™ depend
A.r/
D
A.r
0
/
(9.37)
9.3
Snell's Law
Let us consider now a material such that the
velocity
c
(either ' or “) depends only from the
depth
z
,sothat
s
D
s
(
z
). In this instance, the
quantity: