Geology Reference
In-Depth Information
pulse, such that £(
t
)
C
p
D
£
0
for 0
t
t
0
,
and assuming the initial condition ©(0)
D
0, we
have:
Y
1
e
Yt=2ǜ
£
0
©.t/
D
(7.65)
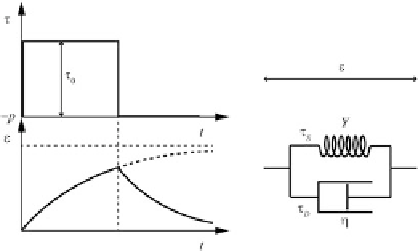
Therefore, the total strain increases progres-
sively (at decreasing rate) towards the asymptotic
value ©(
1
)
D
£
0
/
Y
(Fig.
7.12
). This behavior
implies that the load is initially supported by
the viscous element only, which then elongates
and transfers an increasing amount of stress to
the spring. After a sufficiently long time interval,
most of the stress is supported by the elastic
element. The strain rate associated with creep is
easily obtained by (
7.65
):
Fig. 7.12
Analog model for the Kelvin rheology
which involves displacements on a time scale of
a few tens seconds, and the simultaneous fluid
behavior on a time scale of several tens Myrs
in the context of mantle convection. In general,
the prevalence of elastic behavior with respect to
the viscous response depends from the relative
importance of the parameters
Y
and ǜ.Forlarge
values of the elastic modulus, the material be-
haves as a viscous fluid over long time intervals,
whereas for ǜ
!1
it behaves as an elastic solid
for short-duration loads.
Another important rheological model is the
Kelvin rheology
model, which is also a two-
element system consisting of a linear spring
element and a dashpot, but this time the two
elements are connected in parallel, as shown
in Fig.
7.12
. In this instance, the total
stress
is
partitioned between the spring and the dashpot,
so that:
£
0
2ǜ
e
Yt=2ǜ
P
©.t/
D
(7.66)
Therefore, the strain rate decays exponentially
to zero. Once we have removed the load, at some
time
t
D
t
0
, the subsequent evolution of the strain
field can be determined using the superposition
principle. To set the total stress to zero, we com-
bine the initial stress, £
0
, with an additional stress
field £(
t
)
D
-£
0
,for
t
t
0
. The strain associated
with the initial stress is given by (
7.65
), while that
resulting from the additional stress will be given
by:
e
Y
.
tt
0
/
=2ǜ
1
£
0
Y
©
0
.t/
D
I
t
t
0
(7.67)
Then, for
t
t
0
the total strain follows an
exponential recovery curve:
£.t/
D
£
S
.t/
C
£
D
.t/
(7.62)
Y
e
Yt
0
=2ǜ
1
e
Yt=2ǜ
£
0
where £
S
and £
D
are related to the common strain
© by the following equations:
©.t/
D
I
t
t
0
(7.68)
This solution shows that a Kelvin material has
full strain recovery after load removal. Neither
of the Maxwell and Kelvin models furnishes an
accurate description of the viscoelastic rheology.
For example, the Kelvin model does not exhibit
instantaneous strain after loading or unloading,
and does not account for permanent strain after
relaxation. Similarly, the Maxwell model does
not allow time-dependent recovery and predicts
constant strain rate under constant stress, whereas
£
S
.t/
D
Y©.t/
£
D
.t/
D
2ǜ
P
©
.t/
p
(7.63)
Therefore:
Y
2ǜ
©.t/
D
1
2ǜ
Σ.t/
C
p
P
©.t/
C
(7.64)
This is the constitutive equation associated
with the Kelvin rheology model. For a stress