Geology Reference
In-Depth Information
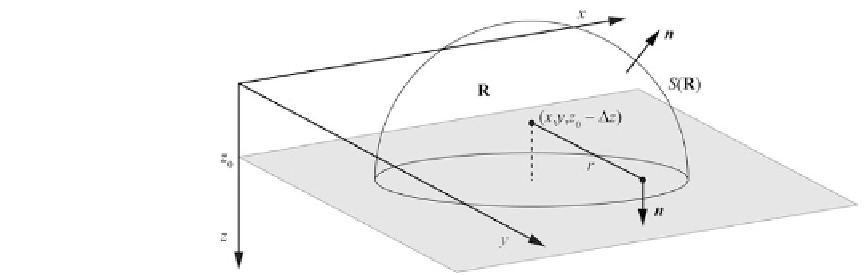
Fig. 5.23
Geometry for
the upward continuation
transformation
if we let the hemisphere radius to increase indef-
initely, the integral over the hemisphere surface
goes to zero, so that the Green third identity
assumes the form:
V.P/
I
U
C
@V
U
C
dS
1
4
1
r
@n
V
@
1
r
D
@n
S.
R
/
(5.86)
V.x;y;
z
0
z
/
"
1
r
To eliminate the first part of the integrand,
we must find a harmonic function
U
such that
U
C
1/
r
D
0on
S
(
R
). It is easy to verify that the
function:
U
x
0
;y
0
;
z
0
LJ
LJ
LJ
LJ
z
0
V
x
0
;y
0
;
z
0
C
Z
C
Z
1
4
@V
@
z
0
D
1
1
#
dx
0
dy
0
LJ
LJ
LJ
LJ
z
0
1
r
@
@
z
0
(5.85)
h
x
x
0
2
C
z
0
C
z
z
0
2
i
1=2
C
y
y
0
2
r
D
[(
x
-
x
0
)
2
C
(
y
-
y
0
)
2
C
(
z
0
-
z
-
z
0
)
2
]
1/2
.
D
where
This
expression
cannot
be
easily
evaluated,
1
¡
x
0
;y
0
;
z
0
because
the
vertical
derivative
of
V
is
not
(5.87)
generally available.
To understand how we can eliminate @
V
/@
z
0
in (
5.85
), let us consider a new harmonic func-
tion
U
in
R
. If we apply the second Green's
obtain:
is harmonic in
R
and satisfies the required con-
dition
U
C
1/
r
D
0 on the plane
z
0
D
z
0
.Further-
more,
U
(
x
0
,
y
0
,
z
0
)
!
0 on the hemisphere surface
as its radius increases. Therefore, substituting
(
5.86
)and(
5.87
)in(
5.85
)gives:
LJ
LJ
LJ
LJ
z
0
C
Z
C
Z
1
r
V
x
0
;y
0
;
z
0
@
@
z
0
1
4
1
¡
dx
0
dy
0
V.x;y;
z
0
z
/
D
1
1
V
x
0
;y
0
;
z
0
C
Z
C
Z
z
2
C
z
2
i
3=2
dx
0
dy
0
D
(5.88)
h
.x
x
0
/
2
C
.y
y
0
/
2
1
1
a plane, given the values on that level surface.
Clearly, in practice the numerical evaluation of
This is the upward continuation integral. It al-
lows to calculate the potential at any point above