The Geomagnetic Field - Quantitative Plate Tectonics - page 107

Fig. 4.4 Flow lines of the magnetic field produced by
a solenoid when a current passes through it. A path, C ,
can be used together with Ampere's law to determine the
magnetic field within the solenoid

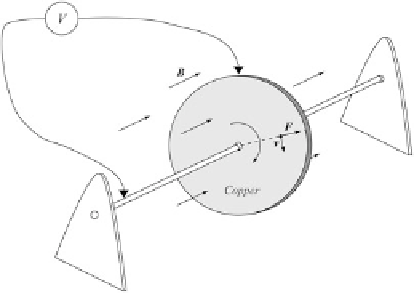
Fig. 4.3 A rotating disk placed in a constant and uniform
magnetic field produces an emf, which can be measured
by the difference of potential, V , between the centre and
the periphery of the disk

I Z

B dr D r B dS

C S.C/

D 0 Z
S.C/

j dS D 0 I.S/ (4.32)

being the distance from the rotation axis. Because
¨ and B have the same direction, a unit charge
at distance r will be subject to a Lorentz force F
D vB D ¨ rB , directed radially toward the disk
border. The total emf can be obtained integrating
over the disk radius, a :

where we have used ( 3.3 ) . This is the integral
form of Ampere's law. It states that the closed
loop integral of the magnetic field is always
proportional to the current flowing through an
arbitrary surface bounded by C . When we apply
( 4.32 ) to the loop C in Fig. 4.4 , we note that C has
an edge of length a within the solenoid, running
parallel to B , two edges that are perpendicular to
B , and one edge outside the wire, where the field
strength is negligible. If I is the current flowing
through the coil and M is the number of turns
for a length a , then the current passing through a
surface bounded by C is MI . Therefore, applying
( 4.32 )wehave:

Z Z

a a

1
2 ¨Ba 2

E D v Bdr D ¨B rdr D (4.30)

0 0

Clearly, we have also a constant magnetic flux
through the disk surface, given by:

ˆ D Ba 2 (4.31)

Thus, it is possible to have a non zero emf
even in presence of constant flux. Another in-
teresting phenomenon occurs when we consider
a solenoid (Fig. 4.4 ). This is a coil wound into
a tightly packed helix, having a diameter small
with respect to its length. When a current passes
through the coil, the resulting magnetic field is
rather intense and uniform within the helix and
negligible outside, with flow lines that are almost
parallel to the solenoid axis (the divergence of B
must be zero everywhere). To calculate the field
within the solenoid, we can apply the integral
version of Ampere's law ( 3.27 ) to the closed loop
C in Fig. 4.4 . Taking the line integral of B along
an arbitrary closed loop C gives:

I

0 MI D B dr Š Ba (4.33)

C

Consequently, the field within a solenoid is
approximately given by:

B Š 0 nI (4.34)

where n D M / a is the number of turns per unit
length. In so far as the number of turns tends to
infinity, solution ( 4.34 ) tends to be an exact so-
lution. Conversely, for a finite solenoid the axial
magnetic field in proximity of the two ends is half