Image Processing Reference
In-Depth Information
Fig. 10.18
Local configurations of middle cells and middle edges in hexagonal grids
compound of all the building blocks we have introduced throughout the chapter, but
we now show explicitly how these building blocks needs to be linked:
⊧
⊨
0
if
x
∈
P
;
dist
t
+
1
(
x
)=
dist
t
(
x
)+
1mod3
if
x
∈
P
∧∀
y
∈
N
(
x
)
;dist
t
(
y
)=
dist
t
(
x
)
;
⊩
dist
t
(
x
)
if
x
∈
P
∧∃
y
∈
N
(
x
)
;dist
t
(
y
)
=
dist
t
(
x
)
;
{
z
∈
N
(
x
)
|
dist
t
(
z
)=
dist
t
+
1
(
x
)
−
1
}
diam. 2 ;
cent
t
+
1
(
x
)=
∃
y
∈
N
(
x
)
;
{
z
∈
N
(
xy
)
|
dist
t
(
z
)=
dist
t
(
xy
)
−
1
.
5
}
diam. 3 ;
back
t
+
1
(
x
)=
cent
t
+
1
(
x
)
∨∃
y
∈
N
(
x
)
;dist
t
(
y
)=
dist
t
(
x
)+
1mod3
∧
back
t
(
y
)
;
conv
t
+
1
(
x
)=
back
t
+
1
(
x
)
∨∃
y
0
,
y
1
∈
N
(
x
)
;conv
t
(
y
0
)
∧
conv
t
(
y
1
)
∧
x
∈
[
y
0
,
y
1
]
.
Here the metric Gabriel centers detection is written using two cases: one for di-
ameters of even length, and the other for the diameters of odd length. In the first
case, it is sufficient to look at the minimally-valued neighbors (those having value
dist
t
+
1
(
1) and to check if they can be separated in two sets of distance 2, i.e.
the diameter of the neighborhood. For the second case, the center is between two
cells
x
and
y
, and we need to look at the “neighborhood of the edge
x
)
−
(
x
,
y
)
”ofra-
dius 1
.
5. So
N
(
xy
)
is a shorthand for
N
(
x
)
∪
N
(
y
)
, and dist
t
(
xy
)
is a shorthand for
min
which is the distance of the edge to the closest
seeds. If the minimally-valued neighbors (those having value dist
t
(
(
dist
t
(
x
)+
0
.
5
,
dist
t
(
y
)+
0
.
5
)
5) can be
separated in two sets of distance 3 (the diameter of the neighborhood), then
x
is the
extremity of an edge-like metric Gabriel center. For concreteness, Fig. 10.18 shows
the set of minimally-valued neighbors that can be separated in two sets whose dis-
tance is the diameter for the case of the hexagonal cellular space. The first line is for
cell-centers, and the second line for edge-centers.
The evolution of this cellular automaton for hexagonal cellular space and with-
out the conv field was already shown in Fig. 10.12. The reader can now recheck the
detection of the middles in the light of our explanation of the relation with metric
Gabriel graphs, balls and centers. When it comes to the number of states, there are
two things to say. Firstly, when restricting to the content of this chapter, namely the
construction of the convex hull for a statis set of seeds, it is not useful to distinguish
between cells having been marked the cent, back and conv rules. These three detec-
tions can be reduced to one Boolean field summarizing the five reasons to be marked
as belonging to the convex hull: being a seed, being a cell-like metric Gabriel center,
xy
)
−
1
.










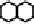






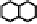

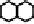

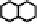










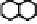


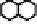


Search WWH ::

Custom Search