Image Processing Reference
In-Depth Information
a Hexagonal
b Hexagonal
c Von Neumann
d Von Neumann
Fig. 10.15
Non-uniquenesses in hexagonal and Von Neumann communication graphs: (a,c)
lines indicate possible shortest paths, and crosses indicate many possible centers for the balls,
(b,d) the isolated point forms a diameter for the ball with any of the other points
have these uniqueness properties, so a generalization of the original definition is
needed.
Indeed, the connectedness of the original definition mainly relies, by definition,
on the existence of sufficiently many Gabriel discs and associated centers. In an
Euclidean space, for a given arbitrary disc and a given point on the border of this
disc, there is a unique diameter segment. Also, for any pair of points, there is a single
disc using these points as diameter. Unfortunately, considering cellular spaces, and
replacing the notion of disc by the metric notion of balls does not conserve these
uniqueness properties as shown in Fig. 10.15. A
ball
is given by a center point and a
radius and corresponds to the set of points of the space whose distance to the center
point is less or equal to the radius. Looking at (b) and (d), we can see that for a given
ball of arbitrary radius
r
, and one selected cell of its left border, there are many cells
on the right forming a diameter for the ball: any of them is at distance 2
r
from the left
cell and, as a consequence, has a shortest path joining it with the left cell and passing
through the center of the ball. In the same vein, a pair of cells is not a diameter for a
unique ball. Indeed, the uniqueness of this ball in Euclidean space is implied by the
uniqueness of the shortest path linking two points. When many shortest paths exist
between two points, they may have different middles, which leads to different balls,
all having the same radius, but each being centered at a different middle as shown
in (a) and (c).
Because of these differences between the Euclidean and cellular case, the orig-
inal Gabriel graph definition in terms of discs does not correspond to a connected
graph in the cellular case. Figure 10.16 gives an example of loss of connectedness
due to the fact that there might be no ball having only two seeds. In (a), every ball
containing two seeds contains an additional third seed, preventing the two points to
have a Gabriel edge. In (b), every ball containing two seeds of different lines con-
tains four additional seeds, preventing the lines to be belong to the same connected
Gabriel component, and so on.
10.5.2.2
Metric Gabriel Graphs
We therefore need to modify the definition to take into account these particularities
in a meaningful way. In [11], an examination of the nature of Gabriel graphs and
its transformation for arbitrary metric spaces is given and the following definition







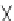
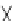















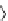









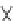


Search WWH ::

Custom Search