Image Processing Reference
In-Depth Information
Fig. 10.9
Evolution of the conv rule with neighborhood radius 1
10.4.2
Complete Metric Convex Hulls
Now that we know how to obtain partial metric convex hulls, involving only shortest
paths of length at most 2, let us target the detection of shortest paths of arbitrary
length. Our first goal is, given two seeds, to select the shortest paths joining them,
i.e. all cells of their interval. A first idea might be to compute the distance of all
cells to all the seeds and then select the cells where the triangle equality is verified.
However we can not handle an arbitrarily large number of integers in each cell in
the cellular automata framework. The number of states of the cells has to be finite.
We can reduce this idea and only store in each cell one distance, the distance to
the closest seeds, modulo 3. This information is, in fact, enough to detect the middles
of the shortest path, and from them, the entire shortest path. A rough intuition for
the latter is given by the fact that, along any shortest path connecting two seeds,
the distance modulo 3 values stored in the cells is
)
for instance. It is possible to locally distinguish between the middle and the non
middle cells, and from these middles, it is possible to join the seeds by following
the distance values in decreasing order
(
0
,
1
,
2
,
0
,
1
,
2
,
0
,
2
,
1
,
0
,
2
,
1
,
0
(
2
,
1
,
0
)
. This is explained in more details in
Sect. 10.4.2.1.
In Sect. 10.4.2.2, we explain that this interval detection is, in fact, enough to solve
entirely the problem and we examine why this is the case. In fact, when many seeds
are involved, sufficiently many pairs of seeds are connected to allow the conv or
majo rules to complete the job. But the investigation of the detection of middles in
general cellular spaces of arbitrary dimensions leads to a trip through the notions of










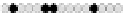




















































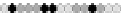











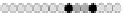









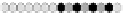





























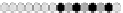





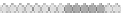



















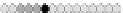




























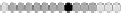








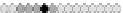



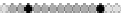



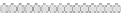











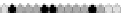
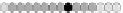
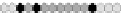
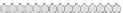



















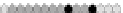


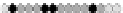
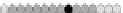






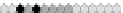































Search WWH ::

Custom Search