Image Processing Reference
In-Depth Information
Fig. 10.8
Distances between cells in a neighborhood
and take one cell
y
in it, we can assign to all cells
z
its distance
d
to
y
as
depicted in Fig. 10.8. If
y
is the center
x
, then all of its neighbors are at distance 1 by
definition, as shown in the first, third, and sixth neighborhoods of Fig. 10.8. If
y
is a
neighbor of the center
x
, then the direct neighbors of
y
are at distance 1 from
y
and
any other cell
z
is at distance 2. Indeed, in this last case, the path
(
y
,
z
)
(
,
,
)
is a shortest
path of length 2. Now, what is the relation with the majority rule ? The answer is
that any time the majority rule selects a cell, it is because half of its neighborhood
is already selected as specified in Sect. 10.2. But this implies that there are two
selected cells of distance 2 apart from each other. This means that there is a shortest
path joining these two cells and passing through the center as we just pointed out.
Therefore the center has to be selected for the set of selected cells to have a chance
of being metric convex. This explains why the majority rule never produces more
than the convex hull, and evolves toward convexity.
Using this understanding, we can replace the majority rule with a more direct one
that checks for the existence of two selected cells in the neighborhood such that a
shortest path passes through the center:
y
x
z
conv
t
+
1
(
x
)=
x
∈
P
∨∃
y
0
,
y
1
∈
N
(
x
)
;conv
t
(
y
0
)
∧
conv
t
(
y
1
)
∧
x
∈
[
y
0
,
y
1
]
;
(10.2)
Note that there are many ways to write this rule formally, but this one is the more
direct one with respect to our intention. Therefore, this formula remains unchanged
if we change the neighborhood in size or shape for example, while other ways of
writing it might need some adaptation.
With this rule, we obtain for example the evolution depicted in Fig. 10.9. The
conv rule has roughly the same global behavior than the majority rule presented
in the sense that it generally produces a set of partial convex hulls and that the
partial convex hulls can merge to form bigger convex hulls during the evolution.
However it has at least two benefits. Firstly, the conv rule is more precise than majo.
Indeed, it detects strictly more neighborhoods than the majority rule. As an example,
one can note that the initial configuration of Fig. 10.9 is a fixpoint for the majority
rule. Secondly, the final result has a clear property that can be expressed without
reference to fixpoints: any shortest path of length 2 between any two cells of the
selected region belongs to the selected region. The link with the convex hull is far
more obvious in this way.





















































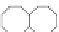



























Search WWH ::

Custom Search