Image Processing Reference
In-Depth Information
c Moore-
√
2
a Von Neumann
b Moore
d Hexagonal
Fig. 10.6
Intervals for different cellular spaces and different metrics
correspond to the communication graph of the Moore cellular space with the length
of diagonal assigned the value
√
2 instead of just 1 as graph metric would imply.
This difference makes the horizontal and vertical edges shorter, and therefore more
preferable than diagonal one. This discards some paths of the Moore cellular space
as being shortest. The structure of the intervals dictates the structure of the metric
convex hulls. Examples of metric convex hulls are shown in Fig. 10.7. This shows
that the definition of metric convex hull is strictly more general than
-convex hull
since the 90, 45, and 60-convex hull corresponds to the metric convexity in Von Neu-
θ
mann, Moore-
√
2 and hexagonal cellular spaces respectively. Note that the Moore-
√
2 can be constructed as the intersection of the Von Neumann and Moore metric
convex hull. This allows us to restrict our attention only to Von Neumann, Moore
and Hexagonal cellular spaces, i.e. we will always consider just plain graph metric,
i.e. the distance between a cell and one of its neighbor is always 1, even for Moore
diagonals. This sets precisely what our goal is: to understand the majority rule based
on metric convexity and to find a cellular automaton that computes this metric con-
vex hull for arbitrary sets of seeds. Because of the chosen level of generality, the
results will also be applicable for a large class of cellular spaces, including 3D and
higher dimensional cellular spaces, but those are unfortunately not very good as
paper examples.
10.4.1
Majority Rule and Metric Convexity
Coming back to what we already said, computing the convex hull is about adding all
the missing shortest paths. In fact, the majority rule can be understood in these terms.
To see that, let us consider the neighborhood
N
of the center cell
x
and the
distance function restricted to this neighborhood. If we take a such neighborhood
(
x
)
∪{
x
}
c Moore-
√
2
a Von Neumann
b Moore
d Hexagonal
Fig. 10.7
Convex hulls for different cellular spaces and different metrics












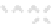




















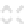






















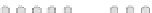





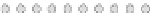


































































































































































































































































Search WWH ::

Custom Search