Convex Hulls and Metric Gabriel Graphs - Cellular Automata in Image Processing and Geometry - page 178

b

a

d

c

g

e

h

f

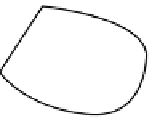
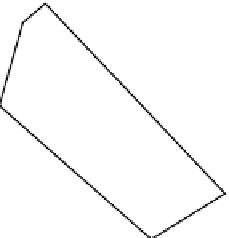
Fig. 10.1 Examples of Euclidean convex and non Euclidean convex shapes

together with a specified neighborhood is called the cellular space. Cells are some-
times called points. The value associated by a configuration c at a cell x is denoted
c

. The configuration obtained at time t by a rule f is denoted f t , subscripts being
used to reduce the impact of repeating the timing information. Hence, f t (

( x )

is the
value associated to a cell x at a time t by a rule f and the transition function of the
rule, for example the sum of all the values in the neighborhood, can be denoted as
f t + 1 (

x )

. Note that we do not indicate explicitly what is the initial
configuration, letting it free to be initialized externally in some sense. Also, rules
are often called fields, similarly to electric field and magnetic field. A single cel-
lular automaton can be made of a certain number of fields, in which case they can
refers to each other in their transition function, and even to just computed values.
For example if there are two rules f and g , f t + 1 (

x )= ∑ y ∈ N ( x ) f t ( y )

as long
as there are no circular definition and everything is well-defined. This is why we
need to be explicit about the timing information. This is a light notation related to,
although a bit more explicit than, the one used in multivariate differential calculus
for example.

x ) might depend on g t + 1 ( x )

10.2 Introduction

The convex hull construction is well known in the context of Euclidean geometry.
Its definition comes in two steps, one for the word “convex” and one for the added
word “hull”. A set of points is convex if and only if it contains entirely any seg-
ment joining any two of its points. As an exercise to link this definition with its
geometrical content, the reader should check, for each shape of Fig. 10.1, whether
the set of its inside points is convex or not by trying to exhibit a segment not entirely
contained in the shape while its extremities are in the shape. Note that some of the
convex shapes are polygons, and others are not.
Convex shapes are simple shapes in some interesting sense. In physics, or physics
simulations for example, detecting when two arbitrary shapes collide is difficult but
this detection is much easier when the shapes are convex. There are also situations