Biology Reference
In-Depth Information
160
140
120
100
80
60
40
20
0
t
1
t
2
t
1
+D
0
10
20
30
40
50
60
Time
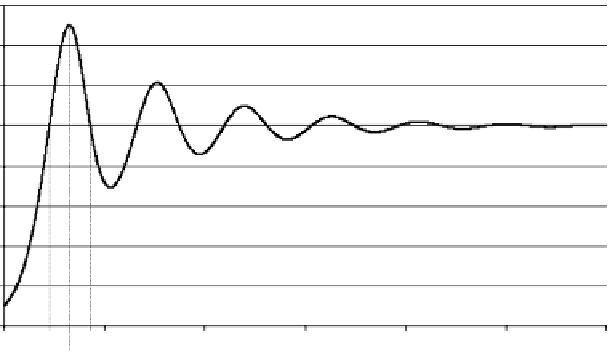
FIGURE 1-22.
A numerical solution of the model described by Eq (1-28). In this case, the delay was D
¼
2.0, and
the parameters were a
¼
0.61; K
¼
100.
enough to solve logistic model (1-24) and find the unique solution
satisfying the initial condition P(0)
P
0
. A computer-generated solution
of Eq. (1-28) is presented in Figure 1-22.
¼
The pattern of convergence to the equilibrium state P
K through
oscillations with decreasing amplitudes (damped oscillations) is similar
to one of the solution trajectories observed in the discrete Verhulst model
[see Figure 1-19(B)]. The heuristic reason for the oscillations is also
essentially the same. The net per capita growth rate used to determine
the population's rate of change at time t uses information on the
availability of resources based on population size at D units of time
earlier. This causes over- or underestimating of the slope while the
system adjusts itself, leading to damped oscillations about the carrying
capacity K. Exercise 14 provides greater insight into the mathematical
properties that allow oscillations to develop in the solution time
trajectories.
¼
E
XERCISE
1-14
Follow the steps outlined below to show that the sign of the derivative
dP/dt in Eq. (1-28) may change over time, causing oscillations.
(a) Assume that at a moment t
1
, the population reaches its carrying
capacity [that is, P(t
1
)
¼
K] and for t in the interval (t
1
, t
1
þ
D)
P(t - D) <K, as in Figure 1-22. Then for t<t
1
þ
D,1-P(t - D)/K
>
0.
Now use Eq. (1-28) to show that for t<t
1
þ
0, and
population size is increasing. In particular, population size is still
increasing at t
D, dP(t)/dt
>
¼
t
1
, thus overshooting the carrying capacity K.