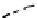Biology Reference
In-Depth Information
700
600
500
400
300
200
100
0
0
2
4
6
8
10
12
14
16
18
Time
FIGURE 1-7.
Comparison of logistic model and actual yeast population growth. Numerical solution of the logistic
model from Eq. (1-12) with a
¼
0.543 and K
¼
660 (dashed line) and yeast growth data (solid line).
introduced by the Belgian mathematician Pierre-Fran¸ois Verhulst in
1845, and are also referred to as ''logistic shapes.'' In terms of their
specific meaning and analytic expressions, however, these curves
may be quite different. We have to be careful, therefore, not to
assume these functions have the same analytic form as (1-13) simply
because their graphs appear similar to the solution of the logistic
equation.
V. AN ALTERNATIVE DERIVATION OF THE LOGISTIC
MODEL
In the previous section, we derived the logistic model based on the
assumption there is a maximum population the environment can
sustain, reflecting limited available resources. In this section, we build a
model to determine the carrying capacity based on maximum available
resources and consumption rates. To keep the model as simple as
possible, we assume a single essential resource. We begin by recalling
that the net per capita growth rate is not constant but is population-
dependent, as shown in Eq. (1-9):
dP
dt
¼
ð
ð
ÞÞ
ð
Þ:
r
P
t
P
t
Now, however, we assume that the net per capita growth rate r depends
on the amount of resource available, which, in turn, depends on the
population size: the higher the population, the lower the resource
available. We denote the value of the available resource by R
¼
R(P), and
rewrite Eq. (1-9) as:
dP
dt
¼
r
ð
R
Þ
P
ð
t
Þ: