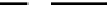Biology Reference
In-Depth Information
The image to have for this dynamic is suggested in Figure 2-21. P(x,y)
denotes the periodic solution. A trajectory that begins inside P will spiral
outward toward P, and one that is outside P, but within the basin of
attraction, will spiral inward toward P. Notice that the theorem says
nothing about how to find the periodic solution.
y
U
P
(
x
,
y
)
(
x
0
,
y
0
)
4. Another Revised Predator-Prey Model
We next present an example showing an application of Poincar´-
Bendixson's criterion. This example comes from Mathematics for
Dynamic Modeling by Edward Beltrami (1987), and illustrates how the
type of equilibrium may change because of changes in the values of the
model parameters.
0
x
FIGURE 2-21.
Graphical representation of the Poincar
´
-
Bendixson's criterion. U is a basin of attraction
and (x
0
,y
0
) is a unique equilibrium point inside U
that is a repeller. Any solution trajectories close
to (x
0
,y
0
) are pushed away from it while forced
to remain in the basin of attraction U. Poincar
´
-
Bendixson's result asserts the existence of a
periodic solution, that is, the existence of a
closed cycle P(x,y) in the phase diagram.
Again, owls (O) are the predators and voles (V) the prey. The
assumption for the voles' growth in the absence of predators is the same
as before (i.e., it follows the logistic equation). We change the
assumption regarding how owls devour voles, so that instead of being
VO
proportional to VO, it is proportional to
V
:
The idea is that an owl
1
þ
can eat only so many voles before becoming sated. The owl then needs
some time to digest before being ready to eat again. So, we have:
dV
dt
¼ a
VO
V
2
V
b
g
V
:
1
þ
We also change the assumptions on the owls' rate of change to the
following:
:
dO
dt
¼ d
e
O
V
O 1
Note that if V were a constant, the above equation would be a logistic
equation for the owls' population growth with a stable equilibrium equal
to V/
. This equation reflects the fact that the carrying capacity of the
predator population is proportional to the number of prey. If
e
0 and
e
O
V
>
d >
1
;
the owls will have a negative per capita growth rate
and will be dying out.
Following Beltrami and Taubes' Differential Equations Modeling in Biology
(Taubes [2001]) and using their choice of constants to facilitate the
computations, we consider the special case:
V
2
6
dV
dt
¼
2
3
V
VO
1
V
¼
f
ð
V
;
O
Þ
þ
0
@
1
A
¼
(2-14)
dO
dt
¼ d
O
V
O 1
g
ð
V
;
O
Þ:
d
As we see next, the stability of this system will depend on the value of
.