Image Processing Reference
In-Depth Information
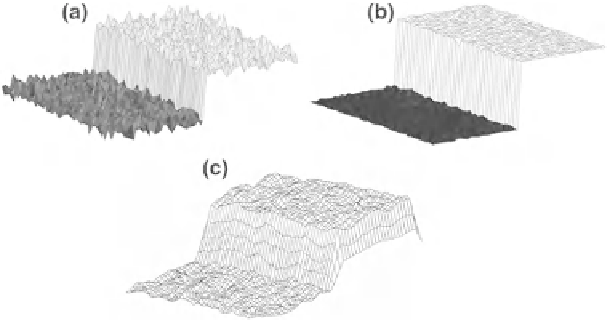
Fig. 3.1
Illustration of bilateral filtering for edge preservation operation.
a
A step edge and its
noisy surroundings,
b
Output, and not output of the bilateral filter, and
c
Output, and not output of
an averaging-based low pass filter
A real time bilateral filter with complexity
has been designed by decompos-
ing into a number of constant time spatial filters in [198]. Porikli has presented three
methods for the computation of constant time bilateral filtering, i.e., with complexity
O(
O(
1
)
. These different implementations are based on polynomial filter expressions,
linear filters, and a Taylor series approximation of bilateral filters, respectively [142].
Very recently Chaudhury et al. have proposed
1
)
O(
1
)
complexity bilateral filter using
trigonometric range kernels [32].
In recent years, several improvements over the original bilateral filter in [175]
have also been suggested. Pham et al. have proposed a separable implementation of
bilateral filter which has been shown to be equivalent to the traditional filtering in
terms of execution time [134]. An adaptive bilateral filter which tunes the parameters
for every pixel based on its perceptual significance has been discussed in [190]. A
trilateral filter which tracks the high gradient region in images by tilting the bilaterally
smoothed image gradient vector has been proposed in [41]. Fattal et al. have applied
a multi-scale strategy for improvement in the performance of bilateral filter [58]. The
equivalence between bilateral filter, and anisotropic diffusion and adaptive smoothing
has already been discussed in [11]. Barash and Comaniciu also proved that bilateral
filter is an extension of the anisotropic diffusion process where the weights have been
chosen with a certain geometrical considerations. Mean shift [43] algorithm can be
employed in the joint spatial-range domains for discontinuity preserving smoothing.
However, when the local mode search space is restricted to the range domain, it is
equivalent to the bilateral filtering [12]. Elad has proved that the theoretical basis for
bilateral filter lies in the Bayesian framework [55]. A recently developed non-local
means filter [19] is a more generalized scheme where the small regions around the
pixels are taken into consideration as opposed to the single pixel values in the case
of bilateral filter during averaging.