Environmental Engineering Reference
In-Depth Information
∂
r
∂
r
y
=
cos
(
MP
,
Oy
)
,
z
=
cos
(
MP
,
Oz
)
,
∂
∂
cos
(
MP
,
l
)=
cos
(
MP
,
Ox
)
cos
(
l
,
Ox
)
+
cos
(
MP
,
Oy
)
cos
(
l
,
Oy
)+
cos
(
MP
,
Oz
)
cos
(
l
,
Oz
)
=
∂
r
∂
)+
∂
r
∂
)+
∂
r
∂
)=
∂
r
∂
x
cos
(
l
,
Ox
y
cos
(
l
,
Oy
z
cos
(
l
,
Oz
l
.
The
u
in Eq. (7.142) is called the
dipole potential
at
M
due to the dipole of
moment
p
at
P
.
Now consider two parallel and very close surfaces
S
and
S
(Fig. 7.6). Their
distance
(
M
)
along the normal is very small. The number of electric charges at any
point on
S
is the same as that at its counterpart point on
S
, but with a negative sign.
Let
n
be the common normal of the two surfaces from the negative charge to the
positive charge. Since
δ
is very small, we may regard
S
and
S
as a surface with two
sides. For a area element d
S
on the surface around point
P
,let
δ
τ
(
)
be its surface
density of the dipole moment. Note that the normal is the dipole-axis. The electric
potential at any point
M
outside the surface due to dipoles on d
S
is thus
P
1
r
PM
d
S
∂
∂
=
τ
(
P
)
cos
(
PM
,
n
)
d
u
(
M
)=
τ
(
P
)
d
S
.
r
PM
n
The potential at
M
due to all dipoles on the surface is,
1
r
PM
d
S
)
∂
∂
τ
(
P
)
cos
(
PM
,
n
)
u
(
M
)=
τ
(
P
=
d
S
.
(7.143)
n
r
PM
S
S
The integral in Eq. (7.143) is called the
double-layer potential
. The single-layer and
double-layer potentials are both called the
surface potential
.
The fundamental solution of Laplace equations is ln
1
r
PM
in two-dimensional
cases. It is the electrical potential of the electric field generated by an infinitely-long
electrified wire with a uniform linear density of electric charges (Section 7.4.1).
Fig. 7.6
Surfaces
S
and
S



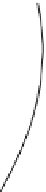






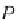




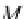

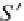











Search WWH ::

Custom Search