Environmental Engineering Reference
In-Depth Information
Here
ρ Δ
x
is the mass of string segment,
F
(
ξ
1
,
t
)
is the mean force density and
2
u
∂
(
ξ
2
,
t
)
is the mean acceleration of the segment. Dividing by
ρ Δ
x
leads to
∂
t
2
2
u
T
ρ
u
x
(
x
+
Δ
x
,
t
)
−
u
x
(
x
,
t
)
F
(
ξ
1
,
t
)
=
∂
(
ξ
2
,
t
)
+
t
2
Δ
x
ρ
∂
By letting
Δ
x
→
0, we arrive at
a
2
u
xx
=
+
(
,
)
,
u
tt
f
x
t
(1.15)
where
a
2
.
Equation (1.15) is the partial differential equation that is satisfied by the vertical
motion
u
=
T
/
ρ
and
f
(
x
,
t
)=
F
(
x
,
t
)
/
ρ
(
,
)
of the vibrating string under an external force (forced vibration). It
is second-order, linear and nonhomogeneous. It is also called the
nonhomogeneous
one-dimensional wave equation
.When
F
x
t
(
x
,
t
)=
0, Eq. (1.15) reduces to
a
2
u
xx
.
u
tt
=
(1.16)
This is the partial differential equation satisfied by the vertical motion
u
of the
vibrating string without external force (free vibration). It is second-order, linear and
homogeneous. It is also called the
one-dimensional wave equation
.
(
x
,
t
)
Remark 1.
Let
L
,
M
and
T
be the unit of length, mass and time, respectively. Thus,
[
L
−
1
,
LT
−
2
. For the wave equations, we obtain
u
x
]=
1,
[
u
xx
]=
[
u
tt
]=
LT
−
2
a
2
L
2
T
−
2
or
LT
−
1
[
f
]=[
u
tt
]=
,
[
]=[
u
tt
]
/
[
u
xx
]=
[
a
]=
.
Hence
a
and
f
have the dimensions of velocity and acceleration, respectively. This
can be further confirmed by their definitions
a
2
. Therefore,
a
represents the
wave speed
. The nonhomogeneous term in Eq. (1.15) is not external
force.
=
T
/
ρ
and
f
=
F
/
ρ
Fig. 1.1
Small transverse displacements of a vibration string














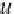
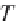











Search WWH ::

Custom Search