Environmental Engineering Reference
In-Depth Information
Remark 2.
The nominal solution contains an exponentially decaying factor in each
term. This relaxes the requirement for the smoothness of the initial distribution
ϕ
(
x
)
in the classical solution. The constraint on
ϕ
(
x
)
is dependent on the existence of the
integral of the product of
ϕ
(
x
)
with the sine function over the domain
[
0
,
l
]
,i.e.the
condition for using the Fourier series to expand.
3.3.2 Uniqueness
The proof of uniqueness and stability is based on the following important physi-
cal phenomenon. Consider one-dimensional heat conduction in a rod without any
internal heat source. Let
M
be the maximum temperature of two ends and initial
distribution. The temperature is then less than or equal to
M
at any point in the rod
and at any time instant. This can be physically understood and can also be proven
mathematically.
Theorem.
Assume that
u
(
x
,
t
)
is continuous in the domain
D
:0
≤
x
≤
l
,
0
≤
t
≤
T
a
2
u
xx
inside
D
.The
u
(
T
is any positive constant; Fig. 3.1) and satisfies
u
t
=
(
x
,
t
)
can then take its maximum or minimum value only at the boundary
Γ
:
x
=
0
,
x
=
l
,
t
=
0. This is called the
extremum principle of heat conduction
.
Proof.
Without loss of generality, we consider the case of maximum value only. We
must then start from the given condition to arrive at
max
D
u
(
x
,
t
)=
max
Γ
u
(
x
,
t
)
(3.21)
,
M
M
. There would exist one point
Let
M
=
max
D
u
(
x
,
t
)
=
max
Γ
u
(
x
,
t
)
. Suppose
M
>
(
x
0
,
t
0
)
inside
D
such that
M
max
D
u
(
x
,
t
)=
u
(
x
0
,
t
0
)=
M
>
.
Define a new function
v
(
x
,
t
)
by
Fig. 3.1
Domain
D










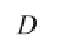
Search WWH ::

Custom Search