Environmental Engineering Reference
In-Depth Information
gration and obtain
s
u
2
N
0
m
i
u
u
!
d
2
N
0
T
e
1
exp
e
1
2
dx
T
e
2
e
m
i
C
4
π
C
4
π
D
0.
(5.118)
This solution describes a solitary wave because, according to the boundary con-
ditions, the perturbation tends to zero at large distances. The solution allows one
to determine the shape of the soliton and the relation between its parameters for
various amplitudes of the wave. We first determine from (5.118) the relation be-
tween the maximum potential of the wave
'
max
and its velocity
u
.Wecandothisby
putting
d
'
/
dx
D
0and
' D '
max
into (5.118). Introducing the reduced variables
mu
2
/(2
T
e
), one can rewrite (5.118) as
D
e
'
max
/
T
e
and
η
D
1
s
1
!
η
1
exp
C
2
η
D
0 .
(5.119)
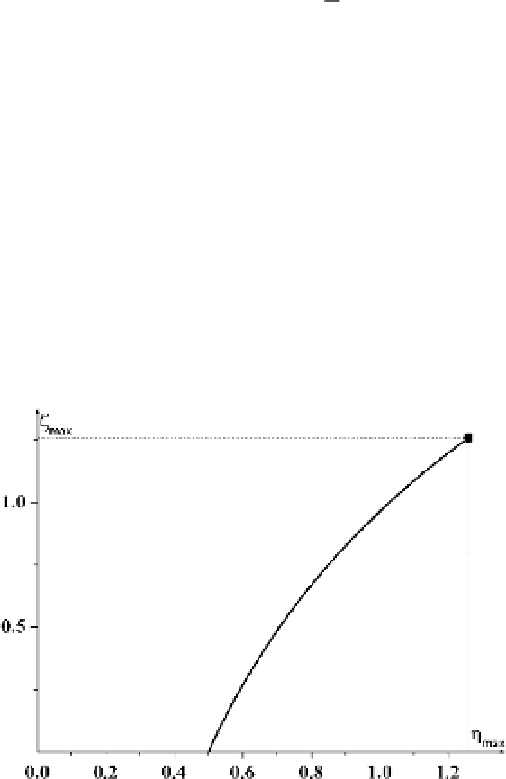
The solution of this equation is given in Figure 5.12. The limiting cases of this equa-
tion are instructive. For a small amplitude of the ion acoustic wave,
!
0, (5.119)
(
T
e
/
m
i
)
1/2
for this wave, corre-
sponding to dispersion relation (5.62) for ion sound of small amplitude. For large-
amplitude waves, (5.119) implies
gives
η
D
1/2. This yields the phase velocity
u
D
D
η
,sotheequationfor
takes the form
1
exp
C
2
D
0 .
(5.120)
1.58(
T
e
/
m
i
)
1/2
.For
larger wave amplitudes the electric potential in the wave center becomes too large
to admit solutions of (5.119), and ions are reflected from the crest of the wave. As a
result, part of the wave reverses and the wave separates into parts. Thus, a solitary
This equation yields
D
1.26, so
e
'
D
1.26
T
e
and
u
D
max
Figure 5.12
The dependence of the maximum reduced electric potential
max
D
e
'
max
/
T
e
on
2
/2
the reduced kinetic energy
η
max
D
m
i
u
T
e
at this maximum.