Environmental Engineering Reference
In-Depth Information
where
B
D
E
a
A
exp(
E
a
/
T
0
)/(
T
0
). Solving this equation with the boundary con-
ditions
X
(0)
D
0,
dX
(0)/
dz
D
0 (the second condition follows from the symmetry
X
(
z
)
D
X
(
z
) in this problem), we have
X
D
2lncosh
z
.
The temperature difference between the center of the gap and the walls is
ln cosh
"
L
2
s
AE
a
2
T
0
#
.
exp
2
T
0
E
a
E
a
2
T
0
Δ
T
T
0
T
w
D
(5.20)
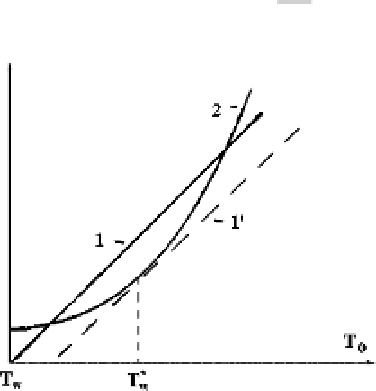
To analyze this expression, we refer to Figure 5.3, illustrating the dependence on
T
0
for the left-hand and right-hand sides of this equation (curves 1 and 2, respec-
tively) at a given
T
w
. The intersection of these curves yields the center temperature
T
0
. The right-hand side of the equation does not depend on the temperature of the
walls and depends strongly on
T
0
. Therefore, it is possible that curves 1 and 2 do
not intersect. That would mean there is not a stationary solution of the problem.
The physical implication of this result is that thermal conduction cannot suffice to
remove the heat released inside the gas. This leads to a continuing increase of the
temperature, and thermal instability occurs.
To find the threshold of the thermal instability corresponding to curve 1
0
in Fig-
ure 5.3, we establish the common tangency point of the curves describing the left-
hand and right-hand sides of (5.20). The derivatives of the two sides are equal when
2
T
0
E
a
Δ
T
D
ln cosh
y
, 1
D
y
tanh
y
,
(5.21)
where
s
AE
a
2
T
0
exp
.
L
2
E
a
2
T
0
y
D
Figure 5.3
The dependence for the right-hand and left-hand sides of (5.20) on the temperature
in the center. The wall temperature
T
w
corresponds to the threshold of the thermal instability.