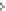Image Processing Reference
In-Depth Information
u
0
u
2
u
u
1
1
1
1
1
···
0
0
0
0
1
1
1
1
u
0
)
u
1
)
u
2
)
(
(
(
8
8
8
?
···
4
4
4
0
0
0
1
1
1
u
n
in
H
1,1
Abbildung 6.17.
Illustration einer Folge
(
)
(]
0, 1
[)
, die die definierende Eigenschaft der Unterhalbst-
→
0
|
verletzt. Wird die Rampe in den Folgengliedern
u
n
bei gleichem Ni-
veauunterschied mit wachsendem
n
beliebig steil, so bilden zwar deren Ableitungen
u
|
d
t
in
L
q
etigkeit für
u
(]
0, 1
[)
u
n
)
)
((
eine beschränkte
Folge in
L
1
, der
L
q
-Grenzwert
u
von
u
n
befindet sich jedoch nur in
L
q
und nicht in
H
1,1
(]
0, 1
[)
(
)
(]
0, 1
[)
(]
0, 1
[)
.
u
n
)
)
nicht in
L
1
Insbesondere konvergiert
((
(]
0, 1
[)
, es stellt sich folglich die Frage, in welchen Sinn man hier
von einem Limes sprechen kann.
n
d
+
1
wobei
∇
ϕ
n
−
1
(
x
)=
∇
ϕ
(
nx
)
. Die Youngsche Ungleichung für die Faltung sowie die
n
−
1
d
k
d
k
k
n
−
k
ergeben
r
d
d
Identitäten
|
B
r
(
0
)
|
=
|
B
1
(
0
)
|
und
(
1
−
)
= ∑
=0
(
)(
−
1
)
u
d
x
d
x
∇
ϕ
1
u
n
Ω
|∇
|
d
x
≤
R
d
|∇
ϕ
n
−
1
|
=
n
1d
x
n
−
1
n
+
1
{
≤|
|≤
}
{
−
n
−
1
≤|
|≤
}
x
1
x
1
n
n
Cn
d
d
k
+1
n
−k
d
k
n
−k
.
−
Cn
1
d
d
1
k
=0
n
−
1
k
k
=1
≤
−
(
1
−
)
=
(
−
1
)
≤
C
+
1
u
n
→
∞
, daher folgt lim inf
n→
∞
Ψ(
)
<
∞
Die rechte Seite ist beschränkt für
n
.
H
1,1
Nun kann aber nicht
u
∈
(
Ω
)
gelten. Wäre dies der Fall, so ergäbe Testen mit
φ ∈D
(
(
))
=
B
1
0
für
i
1, . . . ,
d
u
∂φ
∂
∂φ
∂
d
x
=
d
x
=
∂
Ω
ϕν
i
d
x
=
0.
x
i
x
i
Ω
Ω
Mit dem Fundamentallemma der Variationsrechnung folgte dann
∇
u
|
B
1
(0)
=
0. Analog
bekäme man
∇
u
|
Ω
\B
1
(0)
=
0, damit
∇
u
=
0 fast überall in
Ω
. Das würde aber bedeuten,
dass
u
in
Ω
konstant wäre (siehe Lemma 6.79), ein Widerspruch. Nach Definition von
Ψ(
)=∞
Ψ
ist demnach
.
Wir haben eine Folge
u
n
u
u
n
→
u
gefunden, für die
Ψ
(
u
)
>
lim inf
n→
∞
Ψ
(
)
,
Ψ
i
st
damit nicht unterhalbstetig.
Siehe auch Abbildung 6.17 für eine Veranschaulichung eines Gegenbeispiels zur Un-
terhalbstetigkeit der
H
1,1
-Halbnorm in einer Dimension.
Eine direkte Verallgemeinerung der Sätze 6.84 und 6.86 auf
p
1 ist aufgrund die-
ses Resultats nicht möglich. Analysiert man in Beispiel 6.29 den Beweis für die Un-
terhalbstetigkeit von
F
=
◦
→
A
für
F
:
Y
R
konvex, unterhalbstetig, koerziv und
∞
A
:
X
Y
stark-schwach abgeschlossen, so ist für das Argument essen-
tiell, dass aus der Beschränktheit von
⊃
dom
A
→
Au
n
u
n
(
(
))
(
)
F
für eine Folge
die Existenz einer