Image Processing Reference
In-Depth Information
F
D
F
(
u
)(
v
−
u
)
G
1
G
2
F
v
−
u
u
v
u
K
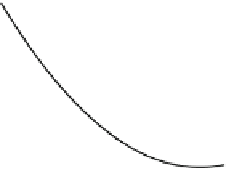
Abbildung 6.7.
Links: Interpretation der Ableitung einer konvexen Funktion in einem Punkt als Steigung der
assoziierten affinen Stützfunktion. Rechts: Außerhalb innerer Punkte des Definitionsbereichs
K
ist die Charak-
terisierung im Allgemeinen falsch: Sowohl
G
1
(
v
)=
F
(
u
)+
D
F
(
u
)(
v
−
u
)
als auch
G
2
(
v
)=
F
(
u
)+
w
(
v
−
u
)
mit
w
>
D
F
(
u
)
lassen sich in
K
durch
F
abschätzen.
Beweis.
Dies folgt aus
u
∗
eingesetzt in (6.8).
=
Für den Spezialfall
K
X
bekommen wir also:
Ist ein Funktional
F
:
X
R
konvex und Gâteaux-differenzierbar, so liegt
ein Minimierer
u
∗
genau dann vor, wenn
→
u
∗
)=
D
F
(
0.
Beispiel 6.36
(Euler-Lagrange-Gleichung für Beispiel 6.1)
Betrachten wir noch einmal Beispiel 6.1, diesmal mit notwendigerweise reellwertigem
u
0
und den entsprechenden reellen Räumen
L
2
R
d
sowie
H
1
R
d
(
)
(
)
. Bezeichnet
F
die
Funktion in (6.1), so ist
F
Gâteaux-differenzierbar mit Ableitung
D
F
)
(
R
d
u
)
v
u
0
(
)=
(
)
−
(
(
)
+
λ
R
d
∇
(
)
·∇
(
)
u
v
x
x
x
d
x
u
x
v
x
d
x
wie wir leicht nachrechnen. Ein optimales
u
∗
kann durch Lösen der D
F
u
∗
)=
(
0 gefun-
den werden, äquivalent dazu ist
R
d
u
∗
(
u
∗
(
R
d
u
0
)
(
)+
λ∇
)
·∇
(
)
=
(
)
(
)
x
v
x
x
v
x
d
x
x
v
x
d
x
H
1
R
d
für alle
v
∈
(
)
. Dies können wir wiederum als schwache Formulierung auffassen
(siehe auch Beispiel 6.4), nämlich von der Gleichung
u
∗
−
λ
Δ
u
∗
=
u
0
in
R
d
.
Die zum Entrauschproblem assoziierte Euler-Lagrange-Gleichung ist also eine partielle
Differentialgleichung. Transformiert man diese in den Frequenzraum, so erhalten wir
)
u
∗
=
u
0
2
(
1
+
λ
|
ξ
|
was schließlich zur schon bekannten Lösung (6.2) führt.