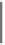Image Processing Reference
In-Depth Information
ϕ
1
2
ϕ
3
1.5
2.5
1
epi
ϕ
1
2
0.5
s
epi
ϕ
3
-2
-1
0
1
2
ϕ
2
x
1
2
2
1
1.5
x
2
-2
-1
0
0
1
2
1
epi
ϕ
2
-1
0.5
-2
s
-2
-1
0
1
2
10
s
2
0
≤
∈
[
−
]
s
0
s
1, 1
1
2
x
1
+
x
2
)
(
)=
(
)=
(
)=
(
ϕ
1
s
ϕ
2
s
ϕ
3
x
1
2
s
2
+
ss
>
0,
∞
sonst,
Abbildung 6.6.
Beispiele für konvexe Funktionen auf
R
und
R
2
.
∈
λ ∈
⊂
für alle
u
,
v
X
und
K
. Hat man einen normierten Raum
Y
mit
Y
X
,so
ist die Einschränkung von
·
Y
fortgesetzt mit
∞
konvex in
X
. Wir schreiben für
∈
u
X
, unter leicht missbräuchlicher Verwendung der Notation,
u
Y
falls
u
∈
Y
,
Y
=
u
∞
sonst.
Es sei noch bemerkt, dass keine Norm auf einem nicht-trivialen normierten Raum
ein strikt konvexes Funktional ist (aufgrund der positiven Homogenität). Die
Situation stellt sich jedoch anders dar für strikt konvexe Funktionen von Nor-
men: Mit
ϕ
:
[
0,
∞
[
→
R
streng monoton steigend und strikt konvex ist
∞
X
genau dann strikt konvex, wenn die Norm in
X strikt konvex
ist, also für alle
u
,
v
)=
ϕ
(
F
u
u
∈
X
mit
u
X
=
v
X
=
1 und
u
=
v
für alle
λ
∈
]
0, 1
[
folgt:
λ
v
X
<
+(
− λ
)
1.
Die Norm eines Hilbert-Raums
X
ist stets strikt konvex, denn für
u
1
u
X
=
v
X
=
λ →
λ
v
2
X
zweimal stetig differenzierbar mit
=
+(
− λ
)
1 und
u
v
ist
F
:
u
1
λ
F
t
2
X
(
λ
)=
−
>
2
u
v
0, also strikt konvex.
3.
Indikatorfunktionale
Das
Indikatorfunktional
einer Menge
K
⊂
X
, d.h.
0
falls
u
∈
K
,
I
K
(
u
)=
∞
sonst.
ist genau dann konvex, falls
K
konvex ist. Solche Funktionale werden verwen-
det, um Beschränkungen in
u
in Minimierungsaufgaben zu realisieren, siehe Bei-