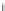Image Processing Reference
In-Depth Information
kleinem
k
den niedrigfrequenten Vektoren
b
−k
entsprechen. Dies ist auch in Abbil-
dung 4.9 zu sehen: Die „hohen“ Basisvektoren haben niedrige Frequenzen, die „mittle-
ren“ Basisvektoren habe die höchsten Frequenzen. Eine weitere Erklärung hierfür lie-
fern das Abtasttheorem und der Alias-Effekt: Bei Abtastung mit Rate 1 ist die höchste
darstellbare Frequenz die Frequenz
und die entspricht dem Vektor
b
n
/2
. Die höheren
Frequenzen werden durch den Alias-Effekt als niedrige Frequenzen abgebildet.
Wenn man die Frequenzdarstellung eines Signals oder Bildes betrachten will, ist es
daher sinnvoll, die Werte der diskreten Fouriertransformation so zu vertauschen, dass
der Koeffizient zur Frequenz Null in der Mitte landet:
π
u
k
u
k
k
k
0
1
2
3
4
5
6
7
-4
-3
-2
-1
0
1
2
3
Auch für die diskrete Fouriertransformation gibt es einen Faltungssatz. Nach der
vorausgehenden Bemerkung ist es nicht verwunderlich, dass er für die periodische Fal-
tung gilt.
Definition 4.47
Seien
u
,
v
C
N
. Die
periodische Faltung
von
u
mit
v
ist
∈
−
N
1
k
=0
v
k
u
(
n−k
) mod
N
.
(
u
v
)
n
=
Satz 4.48
Für u
,
v
C
N
gilt
∈
(
)
n
=
u
n
v
n
.
u
v
N
Beweis.
Die Gleichung lässt sich unter Ausnutzung der Periodizität der komplexen Ex-
ponentialfunktion direkt verifizieren:
l
=
0
v
l
u
(
k−l
) mod
N
exp
−
2
π
i
nk
N
1
k
=
0
−
N
−
1
1
N
(
)
n
=
u
v
N
l
=0
v
l
exp
−
2
π
i
nl
k
=0
u
(
k−l
) mod
N
exp
−
2
π
i
n
(
k
−
l
)
N
−
1
N
−
1
1
N
=
N
N
=
v
n
u
n
.
N
Auch im diskreten Fall lässt sich die Faltung über die Multiplikation der Fourier-
transformierten ausdrücken. Auch hier nennen wir die Fouriertransformation eines Fal-
tungskern die
Transferfunktion
: