Image Processing Reference
In-Depth Information
x
y
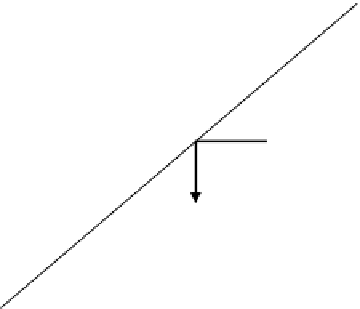
FIGURE 2.64
2.5
Consider a linear, shift-invariant image degradation system with a PSF
h
(
x, y
) ¼
e
2
[j
x
jþj
y
j]
. Suppose the input to the system is an image consisting of
one line as shown in Figure 2.64. What is the output image g
(
x, y
)
?
2.6
Suppose that an image f
(
x, y
)
be
the time-varying components of motion in the x-andy-directions, respectively.
The total exposure at any point of the recording medium (e.g.,
undergoes planer motion, and let x
0
(
t
)
and y
0
(
t
)
film) is obtained
by integrating the instantaneous exposure over the time interval during which
the shutter is open. Then, if T is the duration of exposure, we have
ð
T
1
T
g
(
x, y
) ¼
f
(
x
x
0
(
t
)
, y
y
0
(
t
))d
t
0
where g
(
x, y
)
is the output image.
a. Show that the OTF of the system is
ð
T
1
T
e
j
(v
x
x
0
(
t
)þv
y
y
0
(
t
))
d
t
H
(v
x
,
v
y
) ¼
0
b. Suppose that the image undergoes motion in the x-direction only, at the rate
of x
0
(
t
) ¼
0
:
5at
2
. Sketch the resulting MTF.
2.7
A PSF has no spatial frequencies greater than 400 cycles
=
mm. What values
would you assign to the sampling interval
D
x and the DFT length so as to obtain
samples of the MTF in which aliasing is negligible and samples are spaced no
further than 5 cycles
=
mm apart? The DFT length must be a power of 2.
2.8
Find the Fourier transform of a line oriented at an angle
u
as shown in
Figure 2.65.







Search WWH ::

Custom Search