Information Technology Reference
In-Depth Information
for training and the other half for test (without swapping their roles). We
assume the availability of 2
n
-sized (
X
dt
,T
dt
) sets allowing the computation
of
P
ed
(
n
)
, P
et
(
n
) by simple hold-out for increasing
n
. A consistent learning
algorithm of classifier design will exhibit
P
ed
(
n
),
P
et
(
n
) curves —
learning
curves
—convergingtothemin
P
e
value.
Example 3.6.
We consider the same classifier problem as in Example 3.3. The
results of that example lead us to suspect a convergence of
P
e
towards a value
above 0.2.
We now study in more detail the convergence properties of the MEE linear
discriminant for this dataset, by performing 25 experiments for
n
from 5 to
195 with increments of 10, using simple holdout. The
P
ed
(
n
) and
P
et
(
n
)
statistics are then computed for the 25 experiments.
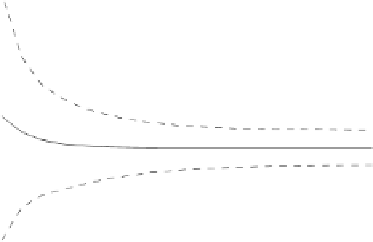
Figure 3.6 shows the learning curves
P
ed
(
n
)
±
s
(
P
ed
(
n
)) and
P
et
(
n
)
±
s
(
P
et
(
n
)), illustrating two important facts:
1. There is a clear convergence of both
P
ed
(
n
) and
P
et
(
n
) towards the same
asymptotic value
P
e
=0
.
237. However, learning is
not
consistent in the
min
P
e
(0.1587) sense. As usual, the convergence of
P
ed
(
n
) is from below
(the training set error rate is optimistic on average) and the convergence
of
P
et
(
n
) is from above (the test set error rate is pessimistic on average).
2. From very small values of
n
(around 50) onwards the
P
et
(
n
)
P
ed
(
n
)
difference is small. The MEE linear discriminant
generalizes well
for this
dataset.
−
0.45
Error rate
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
n
0
0
50
100
150
200
Fig. 3.6 Learning curves for the MEE linear discriminant applied to the Example
3.3 dataset. The learning curves (solid lines) were obtained by exponential fits to
the
P
ed
(denoted '+') and
P
et
(denoted '.') values. The shadowed region represents
P
ed
± s
(
P
ed
)
; the dashed lines represent
P
et
± s
(
P
et
)
.