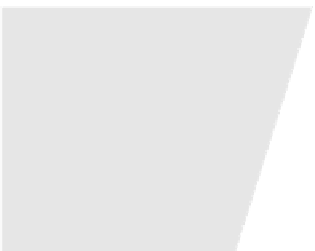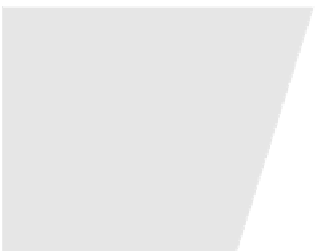Information Technology Reference
In-Depth Information
a
a
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
b
b
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
Fig. 2.11 Wins and losses of MEE and MMSE for two values of
c
(left:
c
=3
;
right:
c
=2
) and a classifier selecting a solution out of two possible ones (see text).
Thetonecodeisasfollows:
- MEE and MMSE both win;
- MEE and MMSE
both loose;
- MMSE wins and MEE looses;
- MEE wins and MMSE looses.
Moreover, for
c
2
.
2 there are no subsets where MMSE wins and MEE loses.
Similar conclusions are reached when the whole interval [
π/
2
,
0] is
considered for
α
. Figure 2.12a shows how
H
S
and
V
vary with
α
when
a
=0
.
95
,b
=
−
1
.
7,and
c
=0
.
9. MEE picks the correct solution, with
min
P
e
=0
.
321, whereas MMSE wrongly selects
α
=
−
0
.
377 with
P
e
=0
.
355.
The curves were obtained by numerical simulation using a large number of
instances (4000 per class) in order to obtain a very close approximation to the
theoretical values of the above formulas. Although not shown in Fig. 2.12a,
MCE also picks the correct solution for these parameter values. For su-
ciently large tails MCE also makes a wrong decision and MEE does not. For
instance, keeping the same values for
a
and
c
(
a
=0
.
95
,c
=0
.
9), the cross-
entropy curve for
b
=
−
−
2
.
4 is shown in Fig. 2.12b. MCE selects
α
=
−
0
.
346
with
P
e
=0
.
411(whereas min
P
e
=0
.
362).
Essentially the same conclusions are obtained if instead of the theoretical
MEE, MSE, and CE risks, we use their empirical estimates.
Note that this example constitutes a good illustration of entropy property
3 (presented in Sect. 2.3.3), explaining the reduced sensitivity of MEE to
tenuous tails.
We then arrive to the conclusion that none of the studied risk functionals
will perform in the optimal min
P
e
sense for all possible classes of problems.
There is also no evidence that any other risk functional we could think of
would always perform optimally in the min
P
e
sense. It then seems advisable
to use classifier learning algorithms employing several types of risk functionals
with different behaviors. As an alternative one could also envisage a meta-
parametrized risk functional emulating the behavior of a whole set of risk
functionals; such an alternative is presented in Chap. 5.