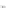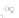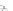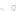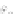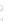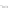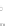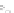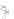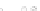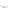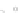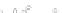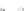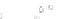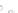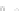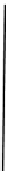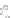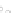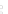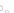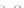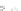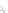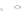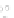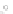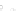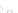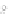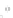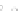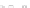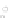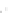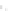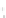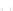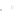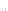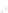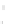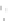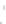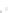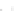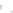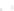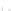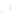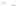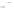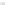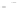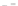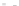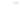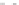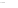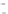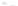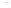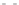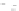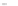Information Technology Reference
In-Depth Information
1
1
1
x
2
x
2
x
2
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
x
1
x
1
x
1
0
0
0
−3
−2
−1
0
1
2
3
−3
−2
−1
0
1
2
3
−3
−2
−1
0
1
2
3
(a)
(b)
(c)
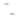
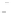
Fig. 2.1 Separating the circles from the crosses by linear regression: a) 600 in-
stances per class; b) 120 instances per class; c) 600 instances per class with noisy
x
2
of class 1. The linear discriminant solution is the solid line.
defining a planar decision surface, has been obtained, we apply the threshold-
ing function, which in geometrical terms determines a linear
decision border
(linear discriminant) as shown in Fig. 2.1.
There are, for this classification problem, an infinity of
f
w
∗
(
x
) solu-
tions, corresponding in terms of decision borders to any straight line in-
side ]
[0
,
1]. In Fig. 2.1a the data consists of 600 instances per
class and the MMSE regression solution results indeed in one of the
P
e
=0
straight lines. This is the large size case; for large
n
(say,
n>
400 instances
per class) one obtains solutions with no misclassified instances, practically
always. Figure 2.1b illustrates the small size case; the solutions may vary
widely depending on the particular data sample, from close to
f
w
∗
(i.e., with
practically no misclassified instances) to largely deviated as in Fig. 2.1b, ex-
hibiting a substantial number of misclassified instances. Finally, in Fig. 2.1c,
the same dataset as in Fig. 2.1a was used, but with 0.05 added to component
x
2
of class 1 ('crosses'); this small "noise" value was enough to provoke a
substantial departure from a
f
w
∗
solution, in spite of the fact that the data
is still linearly separable. The error rate in Fig. 2.1c instead of zero is now
above 3%.
−
0
.
05
,
0
.
05[
×
Example 2.2.
Let us assume a univariate two-class problem (input
X
), with
Gaussian class conditionals
f
X|
0
(left class) and
f
X|
1
(right class), with means
0 and 1 and standard deviation 0
.
5. The classifier task is to determine the
best separating
x
point. Such a classifier is called a data splitter. With equal
priors the posterior probabilities,
P
T |x
, of the classifier (see formula (1.6)) are
as shown with solid line in Fig. 2.2. Note that by symmetry
P
0
|x
=1
−
P
1
|x
and the min
P
e
split point (the decision border) is 0
.
5.
Now suppose that due to some implementation “noise” one computed pos-
teriors
P
T |x
with a deviation
δ
such that
P
1
|x
=
P
1
|x
−
[
P
−
1
δ
for
x
∈
1
|x
(
δ
)
,
0
.
5]
P
−
1
and
P
1
|x
=
P
1
|x
+
δ
for
x
1
|x
(
δ
)].Below
δ, P
T |x
=0,andabove
∈
]0
.
5
,
1
−
P
−
1
P
1
|x
and
δ
=0
.
01 (
P
−
1
1
|x
(
δ
)
,P
T |x
=1.With
P
0
|x
=1
1
0
.
64)
we obtain the dotted line curves shown in Fig. 2.2. The new
P
T |x
are perfect
legitimate posterior probabilities and differ from
P
T |x
no more than 0.01.
−
−
1
|x
(
δ
)=
−