Modellierung lernender Systeme durch Neuronale Netze (NN) - Modellierung komplexer Prozesse durch naturanaloge Verfahren - page 128

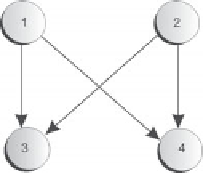
Bild 4-7 Feed forward NN mit vier Einheiten
Wir können dabei annehmen, dass die Einheiten 1 und 2 die Eingabeschicht darstellen sowie
die Einheiten 3 und 4 die Ausgabeschicht. Diese Visualisierung lässt sich jetzt sozusagen direkt
in eine strenge mathematische Darstellung, nämlich in einen so genannten Graphen übersetzen:
Unter einem Graphen wird eine Menge von Elementen verstanden, den so genannten Knoten
(englisch edges), die alle oder zum Teil durch so genannte Kanten (englisch vertices) verbun-
den sind. In unserem Beispiel haben wir also vier Knoten und vier Kanten, nämlich die Ver-
bindungen zwischen den Einheiten 1 und 3 sowie 2 und 4. Da es sich um ein feed forward Netz
handelt, gibt es nur diese Kanten, also keine zwischen 3 und 1 oder 4 und 2. Da in diesem Fall
die Richtung entscheidend ist, spricht man von einem gerichteten Graphen (englisch directed
graph) bzw. Digraph.
Da man in der Theorie allgemeiner Strukturen Kanten als spezielle Relationen zwischen zwei
Knoten auffassen kann (genauer gesagt topologische Relationen), lässt sich eine Kante K AB
zwischen zwei Knoten A und B auch schreiben als K AB = (A, B), womit nichts anderes ausge-
drückt wird als dass eben eine solche Kante existiert. Kanten lassen sich demnach darstellen als
Elemente der Paarmenge E u E, wenn E die Menge der Knoten ist und E u E das cartesische
Produkt der Menge E mit sich selbst die Menge aller geordneten Paare (A, B) mit A, B E
darstellt. Der Begriff des „geordneten“ Paares verweist darauf, dass die Reihenfolge der Kno-
ten relevant ist. Wenn wir nun die Menge aller Kanten als V bezeichnen, dann gilt offenbar,
dass V E u E und wir definieren einen gerichteten Graphen G als
G = (E, V). (4.14)
Zwei Graphen G 1 = (E 1 , V 1 ) und G 2 = (E 2 , V 2 ) sind isomorph , wenn es eine bijektive Abbil-
dung gibt, so dass für alle (A, B) E 1 gilt:
f(A, B) = (f(A), f(B)). (4.15)
Anders gesagt: Jede Kante von G 1 wird auf genau eine Kante von G 2 abgebildet. Da f bijektiv
ist, enthalten G 1 und G 2 genau gleich viele Knoten und Kanten; sie sind in einem topologi-
schen Sinne also strukturgleich, auch wenn ihre geometrische Form durchaus verschieden sein
kann. Der Graph unseres obigen kleinen Netzes z. B. ist isomorph zu dem folgenden Graph:
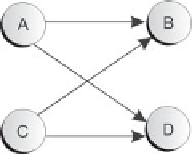
Bild 4-8 Isomorphe Darstellung des Graphen aus Bild 4-7