Geology Reference
In-Depth Information
(a)
Height of
centre of gravity
A
B
C
D
A
B
C
D
(b)
A
Barrier
B
C
D
Time
Time
Time
Spontaneous
fall
Needs push before
spontaneous fall
Spontaneous
fall
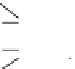
Figure 1.2
Potential energy of a rectangular wooden block in various positions on a planar surface. (a) Four positions of the
block, showing the height of its centre of gravity (dot) in each case. (b) The pattern of potential-energy change as the block
topples, for the unstable (A, C) and
metastable
(B) configurations.
(c) Configuration B presents something of a paradox.
It has a potential energy greater than the unstable
state C, yet, if left undisturbed, it will persist indef-
initely, maintaining the appearance of being stable.
The introduction of a small amount of energy, such
as a person bumping into the table, may however
be sufficient to knock it over. The character of con-
figuration B can be clarified by sketching a graph
of potential energy against time as the block top-
ples over (Figure 1.2b). For both unstable positions
A and C, the potential energy falls continuously to
the value of position D; but in the case of position
B the potential energy must first
rise
slightly, before
falling to the minimum value. The reason is that
the block has to be raised on to its corner (position
A) before it can fall over, and the work involved in
so raising its centre of gravity constitutes a poten-
tial energy 'hurdle' which has to be surmounted
before the block can topple. By inhibiting the spon-
taneous toppling of the block, this hurdle stabilizes
configuration B. One uses the term
metastable
to
describe any high-potential-energy state that is
stabilized by such an energy hurdle.
The application of this reasoning to mineral stability
can be illustrated by the minerals calcite and aragonite,
whose ranges of stability in pressure-temperature
space are shown in the form of a
phase diagram
in
Figure 1.3a. These minerals are alternative crystallo-
graphic forms of calcium carbonate (CaCO
3
), stable
under different physical conditions. The phase diagram
shown in Figure 1.3a is divided into two areas called
stability fields
, one representing the range of applied
pressure and temperature under which calcite is the
stable mineral; the other - at higher pressures - indi-
cating the range of conditions favouring aragonite.
The stability fields are separated by a line, called a
phase boundary
, which defines the restricted set of
circumstances under which calcite
and
aragonite can
coexist together
in equilibrium
with each other.
The energetics of the calcite-aragonite system are
illustrated in Figure 1.3b, which shows how the molar
free energies of the two minerals vary along the line
X-Y in Figure 1.3a. At high pressure (Y), deep within
the crust, the molar free energy of aragonite is less than
that of calcite, and thus aragonite is the stable mineral
under these conditions, analogous to configuration D































Search WWH ::

Custom Search