Geology Reference
In-Depth Information
in km and
x
were measured in hours, the units of
m
would be km hour
−1
and those of c would be km.
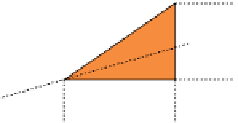
By definition, a straight line has a constant value of
m
throughout its length (variation in the value of
m
is
characteristic of a
curve
). The
x
and
y
coordinates of
any point on the straight line shown in Figure A1(a)
are related by the equation:
How do we measure the gradient (the car's speed) at
a specific point on this curve? Figure A2 shows a por-
tion of the curve enlarged, and we want to measure the
gradient at the point
t
1
. We can begin by determining
the slope of the chord AB, as a first approximation to
that of the curve:
Gradient of chordAB =
δ
δ
y
t
(A3)
=+
(A2)
ymxc
The line shown in Figure A1(a) is said to have a
posi-
tive
gradient; if it sloped in the other direction, so that an
increase in
x
brought about a
decrease
in
y
(negative Δ
y
),
the gradient in Equation A1 would have a
negative
value.
Figure A1(b) shows how positive and negative values of
m
and
c
impact on line orientation and location.
δt
('little delta
t
') represents an
increment
(a small
increase) in
t
, and
δy
is the consequent increment in
y
. If we imagine making
δt
(and consequently
δy
too)
smaller and smaller, the slope of the chord grows
closer and closer to the gradient of the curve at
t
1
. If
we reduce
δt
to the point where it is effectively zero
(written symbolically
δt
→ 0), the chord will coincide
with the tangent
1
to the curve, AC, which by defini-
tion has the same gradient as the curve itself at A.
Expressed in terms of such
infinitesimal
increments,
which are written d
y
and d
t
, the slope of the curve at
point A is:
Gradient of a curve
Many problems in geochemistry require us to deter-
mine the slope or gradient of a curve. The gradient tells
us how rapidly one variable (
y
) is changing in response
to variation in the value of another (
x
) at a particular
point on the curve. If we plot the position
y
of a car
travelling along a straight road against time
t
, for
instance (Figure A2), we get a curve whose gradient at
each point along the curve tells us the car's speed at
the instant concerned: the steeper the graph, the faster
the car was travelling. The horizontal portions of the
curve, on the other hand, indicate when the car was
stationary, for example at a red traffic light.
d
d
y
t
(A4)
Gradient at A
=
Differentiation
This symbolism takes on more meaning when the vari-
ation of
y
with
t
can be expressed in the form of an
equation. Consider a different relationship between
y
and
t,
represented by the equation:
2
y t c
=+
(A5)
We can consider a chord AB analogous to that in the
enlargement in Figure A2. Since point B lies on the
curve, it must also satisfy this equation:
B
(
)
=
( )
+
=+ +
()
+
2
yyat t
+
δ
δ
c
δ
y
C
]
(A6)
2
A
[
at
2
2
at tat
δ
δ
c
δ
t
t
1
Therefore
δy
= 2
atδt
+
a
(
δt
)
2
Time (
t
)
Figure A2
Illustrative plot of a car journey in terms of
distance travelled
y
versus elapsed time.
1
A straight line just grazing a curve, which has the same gradient
as the curve has at the point of contact.














Search WWH ::

Custom Search