Information Technology Reference
In-Depth Information
x,y
x, z
x, y
x, z
x
z
z
x , y
x,y
x, y
x, z
x, z
x, y
x
x
z
z
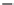
Fig. 9.1
A refutation and a tree-like refutation of the set of clauses
{
x
≥
y
,
x
≥
y
,
x
≥
z
,
x
≥
z
}
≥
≥¯
C
xD
x
.
C
≥
D
≥
≥¯
≥
Cutting variable
x
from clauses
C
D
.
It is easy to see that if a set of clauses
S
is satisfiable and a clause
C
is the resolvent
of two clauses in
S
, then
S
x
and
D
x
we get the
resolvent
clause
C
C
is also satisfiable. A resolution refutation of a CNF
formula
F
is a sequence of clauses
C
1
,...,
∗
C
s
where each
C
i
is either a clause
from
F
or is inferred from earlier clauses by the resolution rule, and
C
s
is the empty
clause (denoted by
can be derived from a set
S
of
clauses by resolution, then
S
is unsatisfiable. In other words, the resolution system
is
correct
. We will soon observe that the system is also
complete
, that is, if a set of
clauses in unsatisfiable then there is always a way to derive the empty clause from it
by resolution.
A resolution refutation can be seen as a directed acyclic graph, a
dag
, in which
the clauses are the vertices, and if two clauses are resolved then there is a directed
edge going from each of the two clauses to the resolvent. If the underlying graph in a
refutation happens to be a tree, we call it a
tree-like
resolution. See Fig.
9.1
. Tree-like
resolution is also a complete refutation system.
). By the above observation, if
Theorem 1.1
Let F be a set of clauses. If F is unsatisfiable, then there is a tree-like
resolution refutation for it.
Proof
We argue by induction on the number
n
of variables in
F
.If
n
1, then there
is only one variable
x
1
and since
F
is unsatisfiable it must contain the clauses
x
1
=