Image Processing Reference
In-Depth Information
essentially in the fact that linguistic characterizations can be less specific than numer-
ical ones and therefore require less information to be used and handled in reasoning
systems.
8.6.1.
Definition
,G,M
) where
x
is the
variable's name,
T
(
x
) the set of values of
x
(referred to as terms),
A linguistic variable is defined by a quintuple (
x, T
(
x
)
,
S
S
is the domain or
the universe in which the values of the variable are defined,
G
is a syntactic rule which
makes it possible to generate the name
X
of each value of
x
and
M
is a semantic
rule, since
M
(
X
) is the fuzzy set defined in
S
that represents the meaning of
X
[DUB 80, ZAD 75, ZIM 91].
This definition represents a symbolic-numerical conversion and establishes ties
between language and numerical scales.
8.6.2.
An example of a linguistic variable
Let us consider the example of an object's size. In numerical terms, this size can be
expressed using a value that varies inside a domain
+
).
In linguistic terms, size can be expressed by using terms such as very small, small,
medium, large, very large, etc. The semantics of these terms are defined by fuzzy sets
in
S
(typically,
S
is a subset of
R
S
. Figure 8.11 illustrates the concept of the linguistic variable “size”.
linguistic variable
size
syntactic rules
terms
{very small, small, medium, large, very large}
semantic rules
M
membership
functions
S
Figure 8.11.
Illustration of the linguistic variable “size”, its terms and the associated fuzzy
sets. The arrows drawn from the linguistic variable to the term set represent syntactic
rules. The second set of arrows represents the semantic rules and translates
the terms into membership functions


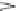


















Search WWH ::

Custom Search