Debris Flows and Landslides - River Dynamics and Integrated River Management - page 253

2002). Similarly, the perturbation equation along the C2-family of characteristic curves is

§ W

U

·

d

( '' u (2 ( gh ) )) ' ¨

0

¹

(4.A11)

¸

d t h

©

m

In a steady laminar flow of a Bingham fluid, the shear stress W 0 is given by (4.A1):

(4.A12)
Figure 4.A1 shows the general velocity distribution of Bingham flow in an open channel. The upper
part is a plug in which the fluid flows at a uniform velocity u p , which is nearly equal to the average
velocity. Only in the zone near the bed does the velocity vary, from zero to u p . The thickness of the layer
is assumed to be į . The velocity gradient, therefore, is roughly u / į , and

W W H

0 B

§ ·

d W u

B

¹

(4.A13)

( '' u (2 gh )) ' K

¨ ¸

d t U h UG h

©

m m

Fig. 4.A1 Velocity distribution of non-Newtonian open channel flow for a Bingham fluid

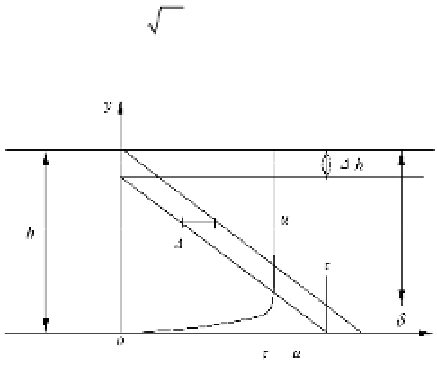
As shown in Fig. 4.A2, a perturbation that occurs at point A ( x , t ) in the x - t plane will propagate along
the characteristic curves AB and AC . For any point B on the C 1 1 characteristic curve that passes through
the point A ( x , t ), a characteristic curve C 2 2 intersects the C 1 1 curve at point B . There is a relation between
' u and at point B (i. e. any point on the C 1 1 characteristic curve).

' (2 ( gh ) )

Fig. 4.A2 Characteristic curves on the x - t plane (The abscissa is the x -axis and the ordinate is the time t -axis). If a
perturbation occurs at the point A , it propagates downstream along the C 1 1 curve and upstream along the C 2 1 curve

The area below the curves CAB is undisturbed. The initial perturbation has no effect on the area, and the
velocity u and depth h remain constant. Integration of Eq. (4.A11) along the C 2 2 characteristic curve yields