Information Technology Reference
In-Depth Information
f
C
(
)
=
(
)
+
(
)
z
f
x
jf
y
(3.3)
where
z
=
x
+
jy
is a complex variable and
f
∈
R
is conventional real-valued
activation function as given below:
1
f
(
x
)
=
(3.4)
e
−
x
1
+
In split activation function, a nonlinear function is applied separately to the real and
imaginary parts of the net potential (aggregation at the input) of the neuron. Here
sigmoidal activation function (Eq.
3.4
) is used separately for real and imaginary
part. This arrangement ensures that the magnitude of real and imaginary part of
f
C
(
is no longer analytic
(holomorphic), because the Cauchy-Riemann equation does not hold:
z
)
is bounded between 0 and 1. But now the function
f
C
(
z
)
∂
f
C
(
z
)
j
∂
f
C
(
z
)
+
= {
1
−
f
(
x
)
}
f
(
x
)
+
j
{
1
−
f
(
y
)
}
f
(
y
)
=
0
∂
x
∂
y
The 2D extension of the real sigmoid function, as in Eqs.
3.3
and
3.4
, always yield
a bounded behavior of activation function
f
C
(
)
. So, effectively the holomorphy is
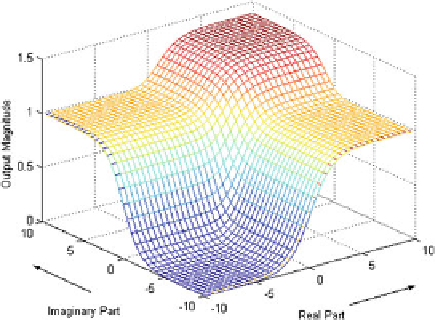
compromised for the boundedness of the activation function. Figure
3.4
shows the
output magnitude of the neuron with respect to the real and imaginary parts of the
input for function definition given in Eq.
3.3
.
It has been proved that CVNN with activation function, Eq.
3.3
, can approximate
any continuous complex-valued function where as the one with a analytic activation
function, Eq.
3.1
, proposed by Kim and Guest in 1990, Haykin in 1991 and tanh
z
)
by Adali in 2000 can not approximate any nonanalytic complex-valued function
[
2
]. Thus, CVNN with activation function, Eq.
3.3
, appeared as a universal approx-
imator in all researches. In 1997, Nitta [
7
] and later Tripathi [
8
,
18
,
24
] has also
confirmed the stability of learning of CVNN with this activation function through
(
z
Fig. 3.4
Output magnitude
of the split-type activation
function



Search WWH ::

Custom Search